 por matmat2 » Dom Mai 30, 2010 21:25
por matmat2 » Dom Mai 30, 2010 21:25
raiz cubica (2x-1) - raiz cubica (x-1) = 1
(2x-1)^1/3 - (x-1)^1/3 = 1
oriunda de ex. de fisica
não consigo desenvolver, as respostas caso ajude são 1 e 2(14+3*raizquadrada 21)
muito obrigado a quem conseguir desenvolver
-
matmat2
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 30, 2010 21:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
 por Mathmatematica » Sáb Jun 05, 2010 05:35
por Mathmatematica » Sáb Jun 05, 2010 05:35
Vamos tentar desenvolver... (Primeiramente, olá.

)
![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png)
Essa é uma equação irracional. Vamos então impor as condições de existência. Como

então devemos ter que
![\sqrt[3]{2x-1}>\sqrt[3]{x-1} \sqrt[3]{2x-1}>\sqrt[3]{x-1}](/latexrender/pictures/7563c2e3b035c741a71ca9a5ed1d22cc.png)
ou devemos ter que
![\sqrt[3]{2x-1}<\sqrt[3]{x-1} \sqrt[3]{2x-1}<\sqrt[3]{x-1}](/latexrender/pictures/4e904686f58eddef150bf17774ff2a21.png)
(pois podemos ter resultados negativos: raiz de índice ímpar). Para o 1º caso temos que
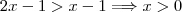
. Mas isso só ocorre se
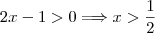 e
e 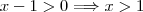
. Fazendo a intercessão (vamos interceder para que eu nunca mais cometa esse erro), digo interseção das inequações teremos que

satisfaz o primeiro caso.
Para o 2º caso temos a inversão das inequações, certo? Sendo assim teremos
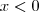 e
e 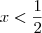 e
e 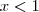
e a interseção dessas condições nos dá
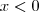
. Se

é solução dessa inequação então
![k\in\mathbb R-[0,1] k\in\mathbb R-[0,1]](/latexrender/pictures/a8f99b6b60e719df037754349b99782c.png)
. Logo a(s) solução(ões) dessa inequação não está entre zero e 1, inclusive.
Vamos aos cálculos:
![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png)
![(\sqrt[3]{2x-1}-\sqrt[3]{x-1})^3=1^3 (\sqrt[3]{2x-1}-\sqrt[3]{x-1})^3=1^3](/latexrender/pictures/f44f4bfa26fca549bd737632cc995370.png)
![(2x-1)-3\sqrt[3]{(2x-1)^2(x-1)}+3\sqrt[3]{(2x-1)(x-1)^2}-(x-1)=1 (2x-1)-3\sqrt[3]{(2x-1)^2(x-1)}+3\sqrt[3]{(2x-1)(x-1)^2}-(x-1)=1](/latexrender/pictures/c2b3ba752c2abb5e22f3b4b2d7cabdd5.png)
![2x-x-1+1-3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})=1 2x-x-1+1-3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})=1](/latexrender/pictures/1429091f075301a44f65f55b33e0ac94.png)
![x-1=3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1}) x-1=3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})](/latexrender/pictures/bb901b1614c6cf6fbf57ef56679e53a4.png)
Da primeira equação (que por sinal é semelhante às demais) temos que
![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png)
. Então:
![x-1=3\sqrt[3]{(2x-1)(x-1)} x-1=3\sqrt[3]{(2x-1)(x-1)}](/latexrender/pictures/483636cd3a7b401ce34219c3f790ad70.png)
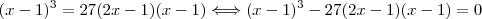
![(x-1)[(x-1)^2-27(2x-1)]\Longrightarrow x-1=0 \ $ou$ \ (x-1)^2-27(2x-1)=0 (x-1)[(x-1)^2-27(2x-1)]\Longrightarrow x-1=0 \ $ou$ \ (x-1)^2-27(2x-1)=0](/latexrender/pictures/48de1d3f57c3c7dfe7bb06fae3795481.png)
Então:
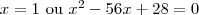

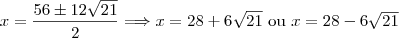
Perceba porém que
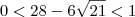
. Então esse resultado não convém, pois não obedece às condições do problema. Sendo assim, os valores de x que satisfazem essa equação são
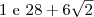
.
Observações:
_Qualquer erro, por favor, AVISEM!!!

-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Socorro que equação é está ??
por oescolhido » Dom Fev 10, 2013 10:11
- 0 Respostas
- 660 Exibições
- Última mensagem por oescolhido

Dom Fev 10, 2013 10:11
Equações
-
- Não consigo resolver esta equação
por Ariel » Seg Nov 09, 2015 19:49
- 4 Respostas
- 3082 Exibições
- Última mensagem por eulercx

Ter Nov 10, 2015 10:52
Álgebra Elementar
-
- [Não estou entendendo esta equação] alguem pode me ajudar??
por teilom » Dom Jul 07, 2013 11:57
- 2 Respostas
- 1994 Exibições
- Última mensagem por teilom

Seg Jul 08, 2013 12:31
Equações
-
- Será que esta relação geométrica esta errada?
 por Guga1981 » Qua Ago 29, 2018 18:51
por Guga1981 » Qua Ago 29, 2018 18:51
- 5 Respostas
- 17619 Exibições
- Última mensagem por Gebe

Sáb Set 01, 2018 22:27
Geometria Plana
-
- Esta minha resolucao está correta?
por SsEstevesS » Dom Nov 27, 2011 10:29
- 0 Respostas
- 2972 Exibições
- Última mensagem por SsEstevesS

Dom Nov 27, 2011 10:29
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 )
)![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png)
 então devemos ter que
então devemos ter que ![\sqrt[3]{2x-1}>\sqrt[3]{x-1} \sqrt[3]{2x-1}>\sqrt[3]{x-1}](/latexrender/pictures/7563c2e3b035c741a71ca9a5ed1d22cc.png) ou devemos ter que
ou devemos ter que ![\sqrt[3]{2x-1}<\sqrt[3]{x-1} \sqrt[3]{2x-1}<\sqrt[3]{x-1}](/latexrender/pictures/4e904686f58eddef150bf17774ff2a21.png) (pois podemos ter resultados negativos: raiz de índice ímpar). Para o 1º caso temos que
(pois podemos ter resultados negativos: raiz de índice ímpar). Para o 1º caso temos que 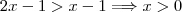 . Mas isso só ocorre se
. Mas isso só ocorre se 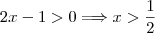 e
e 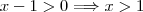 . Fazendo a intercessão (vamos interceder para que eu nunca mais cometa esse erro), digo interseção das inequações teremos que
. Fazendo a intercessão (vamos interceder para que eu nunca mais cometa esse erro), digo interseção das inequações teremos que  satisfaz o primeiro caso.
satisfaz o primeiro caso.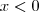 e
e 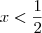 e
e 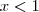 e a interseção dessas condições nos dá
e a interseção dessas condições nos dá 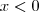 . Se
. Se  é solução dessa inequação então
é solução dessa inequação então ![k\in\mathbb R-[0,1] k\in\mathbb R-[0,1]](/latexrender/pictures/a8f99b6b60e719df037754349b99782c.png) . Logo a(s) solução(ões) dessa inequação não está entre zero e 1, inclusive.
. Logo a(s) solução(ões) dessa inequação não está entre zero e 1, inclusive.![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png)
![(\sqrt[3]{2x-1}-\sqrt[3]{x-1})^3=1^3 (\sqrt[3]{2x-1}-\sqrt[3]{x-1})^3=1^3](/latexrender/pictures/f44f4bfa26fca549bd737632cc995370.png)
![(2x-1)-3\sqrt[3]{(2x-1)^2(x-1)}+3\sqrt[3]{(2x-1)(x-1)^2}-(x-1)=1 (2x-1)-3\sqrt[3]{(2x-1)^2(x-1)}+3\sqrt[3]{(2x-1)(x-1)^2}-(x-1)=1](/latexrender/pictures/c2b3ba752c2abb5e22f3b4b2d7cabdd5.png)
![2x-x-1+1-3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})=1 2x-x-1+1-3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})=1](/latexrender/pictures/1429091f075301a44f65f55b33e0ac94.png)
![x-1=3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1}) x-1=3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})](/latexrender/pictures/bb901b1614c6cf6fbf57ef56679e53a4.png)
![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png) . Então:
. Então:![x-1=3\sqrt[3]{(2x-1)(x-1)} x-1=3\sqrt[3]{(2x-1)(x-1)}](/latexrender/pictures/483636cd3a7b401ce34219c3f790ad70.png)
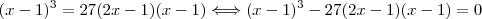
![(x-1)[(x-1)^2-27(2x-1)]\Longrightarrow x-1=0 \ $ou$ \ (x-1)^2-27(2x-1)=0 (x-1)[(x-1)^2-27(2x-1)]\Longrightarrow x-1=0 \ $ou$ \ (x-1)^2-27(2x-1)=0](/latexrender/pictures/48de1d3f57c3c7dfe7bb06fae3795481.png)
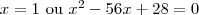

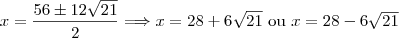
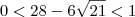 . Então esse resultado não convém, pois não obedece às condições do problema. Sendo assim, os valores de x que satisfazem essa equação são
. Então esse resultado não convém, pois não obedece às condições do problema. Sendo assim, os valores de x que satisfazem essa equação são 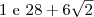 .
.





