 por pondepondeponde » Seg Abr 19, 2010 17:42
por pondepondeponde » Seg Abr 19, 2010 17:42
Olá pessoal,
é a primeira vez que estou postando no blog então desculpem-me se a pergunta for meio ou totalmente tola.
Acontece que estou estudando para uma prova de campos vetoriais (cálculo 3) e quando vou fazer exercícios relacionados à integrais de linha NUNCA consigo enxergar o intervalo à ser utilizado. Fatalmente calculo tudo errado, já que não utilizei o intervalo correto.
Alguém com algum insight? Qual a melhor forma de enxergar os intervalos à serem utilizados?
Nos exercícios abaixo devo calcular a integral de linha por dois métodos (a) diretamente (b) pelo teorema de Green.
Exercício 1.
C é o retângulo com vértices (0,0) , (2,0) (2,3) e (0,3)
integral (orientada positivamente) xy^2 dx + x^3 dy
Exercício 2.
C é o círculo com centro na origem e raio 1
integral (orientada positivamente) y dx - x dy
Muito obrigado!
-
pondepondeponde
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Abr 19, 2010 17:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. vicil
- Andamento: cursando
 por luispereira » Sex Dez 24, 2010 14:14
por luispereira » Sex Dez 24, 2010 14:14
primeiro calcularei pelo teorema de green porque é bem mais rápido de ficar parametrizando. Dado que o teorema de green é uma exceção do thm Strokes,então, so temos que calcular a componente Z do rotacional da função que é:
![[3x^2-2xy]dA [3x^2-2xy]dA](/latexrender/pictures/fce46e545b96343aa07e47ffd7a082c9.png)
integrando para a condição:
![\int^{2}_{0}\int^{3}_{0}[3x^2-2xy]dA \int^{2}_{0}\int^{3}_{0}[3x^2-2xy]dA](/latexrender/pictures/1a150b9ef345a5c212bedab7b1cf8e46.png)
que tem como resposta:
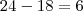
Se estiver errado manda denovo que eu faço com mais calma,flow
-
luispereira
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Dez 23, 2010 18:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Intervalos
por Revelants » Dom Out 05, 2008 15:02
- 1 Respostas
- 2168 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:43
Funções
-
- Intervalos de confiança
por miguel337 » Seg Jul 18, 2011 12:34
- 1 Respostas
- 6664 Exibições
- Última mensagem por Neperiano

Seg Jul 18, 2011 20:39
Estatística
-
- [Intervalos] me ajudem
por suhkaiser » Qui Mai 17, 2012 15:57
- 1 Respostas
- 1091 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 09:11
Funções
-
- determinar os intervalos
por virginia » Sex Abr 26, 2013 14:09
- 1 Respostas
- 1085 Exibições
- Última mensagem por e8group

Sex Abr 26, 2013 17:25
Funções
-
- União de intervalos.
por eu_dick1 » Sex Mai 23, 2014 14:16
- 4 Respostas
- 3436 Exibições
- Última mensagem por alienante

Sáb Mai 24, 2014 21:09
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![[3x^2-2xy]dA [3x^2-2xy]dA](/latexrender/pictures/fce46e545b96343aa07e47ffd7a082c9.png)
![\int^{2}_{0}\int^{3}_{0}[3x^2-2xy]dA \int^{2}_{0}\int^{3}_{0}[3x^2-2xy]dA](/latexrender/pictures/1a150b9ef345a5c212bedab7b1cf8e46.png) que tem como resposta:
que tem como resposta: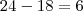
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)