 por Daniella Isadora » Sáb Ago 15, 2015 00:32
por Daniella Isadora » Sáb Ago 15, 2015 00:32
Calcular o limite de:
a) lim
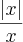
x?0
g) lim
4x ? 1 x?+? 2x ? 5
-
Daniella Isadora
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Ago 15, 2015 00:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por nakagumahissao » Sáb Ago 15, 2015 11:18
por nakagumahissao » Sáb Ago 15, 2015 11:18
Como tive que colocar alguns gráficos, fiz as resoluções no meu site.
Por favor, na proxima vez que for postar alguma coisa, as regras deste fórum pedem que coloque também o que já tentou fazer para resolver o problema para que saibamos quais são realmente suas dúvidas e para que não fiquemos apenas nos sentido "usados" como resolvedores de problemas e trabalhos. O objetivo é ensinar e aprender e não somente resolver problemas.
Veja a resolução em:
http://matematicaparatodos.pe.hu/2015/0 ... a-limites/Grato
Sandro
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Calcular esse limite
 por ViniciusAlmeida » Sáb Abr 18, 2015 08:45
por ViniciusAlmeida » Sáb Abr 18, 2015 08:45
- 1 Respostas
- 1920 Exibições
- Última mensagem por adauto martins

Qui Mai 07, 2015 13:02
Cálculo: Limites, Derivadas e Integrais
-
- CALCULAR LIMITE
por Michelee » Dom Mai 01, 2011 12:04
- 3 Respostas
- 3119 Exibições
- Última mensagem por LuizAquino

Dom Mai 01, 2011 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Calcular limite
por LAZAROTTI » Ter Mai 01, 2012 13:56
- 1 Respostas
- 1367 Exibições
- Última mensagem por LuizAquino

Ter Mai 01, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o limite de
por nowfeer » Seg Jun 18, 2012 01:22
- 2 Respostas
- 1861 Exibições
- Última mensagem por nowfeer

Ter Jun 19, 2012 21:36
Cálculo: Limites, Derivadas e Integrais
-
- calcular o limite de 1/2x
por ricardosanto » Seg Jun 18, 2012 20:10
- 4 Respostas
- 2848 Exibições
- Última mensagem por ricardosanto

Ter Jun 19, 2012 03:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
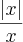

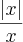


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.