Tenho bastantes dificuldades no exercício seguinte. Alguém me ajuda a resolver?
Eu não consegui resolver este exercício, pois não compreendi ao certo quais os passos a fazer, daí só ter apresentado o exercício em si para que alguém me ajude na resolução do mesmo.
2. "Na figura está parte da representação gráfica da função f , de domínio IR+ , definida por f(x) = ln x (ln designa logaritmo de base e ) .

Os pontos A e C , que pertencem ao gráfico da função f , são vértices de um rectângulo [ABCD] , de lados paralelos aos eixos do referencial.
As abcissas de A e de C são 2 e 6 , respectivamente.
2.1. Determine a ordenada do ponto:
a) A;
b) C.
2.2. Use as propriedades dos logaritmos para escrever na forma de um único logaritmo:
a)
__
CD
b) a área do rectângulo [ABCD]


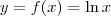 . O ponto A tem abscissa 2, então sua ordenada será:
. O ponto A tem abscissa 2, então sua ordenada será:  .
. .
. . O ponto C, como calculado anteriormente, tem ordenada
. O ponto C, como calculado anteriormente, tem ordenada  . O segmento
. O segmento  tem comprimento
tem comprimento  , logo:
, logo: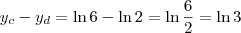
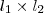 , certo? Nós temos os dois lados, um de comprimento 4 e outro de comprimento
, certo? Nós temos os dois lados, um de comprimento 4 e outro de comprimento 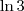 , então:
, então: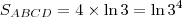


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.