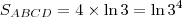por Asustek27 » Dom Mar 14, 2010 19:24
por Asustek27 » Dom Mar 14, 2010 19:24
Boa noite,
Tenho bastantes dificuldades no exercício seguinte. Alguém me ajuda a resolver?
Eu não consegui resolver este exercício, pois não compreendi ao certo quais os passos a fazer, daí só ter apresentado o exercício em si para que alguém me ajude na resolução do mesmo.
2. "Na figura está parte da representação gráfica da função f , de domínio IR+ , definida por f(x) = ln x (ln designa logaritmo de base e ) .

Os pontos A e C , que pertencem ao gráfico da função f , são vértices de um rectângulo [ABCD] , de lados paralelos aos eixos do referencial.
As abcissas de A e de C são 2 e 6 , respectivamente.
2.1. Determine a ordenada do ponto:
a) A;
b) C.
2.2. Use as propriedades dos logaritmos para escrever na forma de um único logaritmo:
a)
__
CD
b) a área do rectângulo [ABCD]
-
Asustek27
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mar 14, 2010 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: cursando
 por MarceloFantini » Dom Mar 14, 2010 23:01
por MarceloFantini » Dom Mar 14, 2010 23:01
Boa noite.
Para encontrar a ordenada, basta substituir na função. Lembre-se que você não precisa dar um valor exato.
O gráfico é
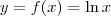
. O ponto A tem abscissa 2, então sua ordenada será:

.
Analogamente para o C:

.
Para a segunda questão, pense nas propriedades do retângulo. O ponto D tem a mesma ordenada que A, portanto

. O ponto C, como calculado anteriormente, tem ordenada

. O segmento

tem comprimento

, logo:
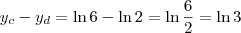
A área é
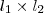
, certo? Nós temos os dois lados, um de comprimento 4 e outro de comprimento
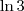
, então:
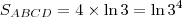
É na verdade apenas um exercício para trabalhar com as propriedades de logaritmo.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Asustek27 » Seg Mar 15, 2010 15:25
por Asustek27 » Seg Mar 15, 2010 15:25
Fantini escreveu:Boa noite.
Para encontrar a ordenada, basta substituir na função. Lembre-se que você não precisa dar um valor exato.
O gráfico é
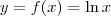
. O ponto A tem abscissa 2, então sua ordenada será:

.
Analogamente para o C:

.
Para a segunda questão, pense nas propriedades do retângulo. O ponto D tem a mesma ordenada que A, portanto

. O ponto C, como calculado anteriormente, tem ordenada

. O segmento

tem comprimento

, logo:
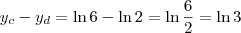
A área é
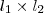
, certo? Nós temos os dois lados, um de comprimento 4 e outro de comprimento
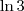
, então:
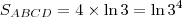
É na verdade apenas um exercício para trabalhar com as propriedades de logaritmo.
Espero ter ajudado.
Um abraço.
Olá Fantini.
Era isso mesmo. Gostava imenso de lhe agradecer a sua preciosa ajuda, pois estava perdido num exercício que vendo agora, era bastante simples.
Grande abraço, alguma coisa que possa ajudar, disponha.
Cumprimentos!
-
Asustek27
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Mar 14, 2010 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Logarítmica
por OtavioBonassi » Qui Jan 06, 2011 21:58
- 12 Respostas
- 8038 Exibições
- Última mensagem por OtavioBonassi

Sex Jan 07, 2011 23:42
Funções
-
- Função Logaritmica
por nessitahfl » Qui Abr 17, 2014 11:06
- 3 Respostas
- 2586 Exibições
- Última mensagem por nessitahfl

Ter Abr 22, 2014 10:48
Funções
-
- Função Logarítmica
por Carlos28 » Sex Mar 13, 2015 10:02
- 2 Respostas
- 2471 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:36
Logaritmos
-
- Função logarítmica
por zenildo » Qua Jul 15, 2015 12:26
- 1 Respostas
- 2058 Exibições
- Última mensagem por nakagumahissao

Qui Jul 16, 2015 14:37
Logaritmos
-
- (AMAN) função logaritmica
por natanskt » Sex Out 29, 2010 10:27
- 1 Respostas
- 1540 Exibições
- Última mensagem por DanielFerreira

Qui Nov 18, 2010 17:46
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



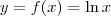 . O ponto A tem abscissa 2, então sua ordenada será:
. O ponto A tem abscissa 2, então sua ordenada será:  .
. .
. . O ponto C, como calculado anteriormente, tem ordenada
. O ponto C, como calculado anteriormente, tem ordenada  . O segmento
. O segmento  tem comprimento
tem comprimento  , logo:
, logo: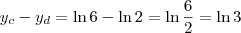
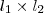 , certo? Nós temos os dois lados, um de comprimento 4 e outro de comprimento
, certo? Nós temos os dois lados, um de comprimento 4 e outro de comprimento 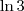 , então:
, então: