 por Dada » Seg Mar 08, 2010 14:05
por Dada » Seg Mar 08, 2010 14:05
E ae pessoal,
a questão é a seguinte:
![z=f(x,y)=ln(y-x^2-2x)+\sqrt[2]{2x-x^2-y} z=f(x,y)=ln(y-x^2-2x)+\sqrt[2]{2x-x^2-y}](/latexrender/pictures/88ef5d5b6edb9517e0f77634b547058a.png)
logo
![Df=\left[(x,y)\epsilon\Re^2/y-x^2-2x>0 e 2x-x^2-y\geq0\right] Df=\left[(x,y)\epsilon\Re^2/y-x^2-2x>0 e 2x-x^2-y\geq0\right]](/latexrender/pictures/b95c988ac257bcdceb955863491e4f0a.png)
e agora vamos esboçar o gráfico
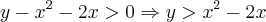
os pontos da parábola onde o gráfico intercepta n deveriam ser

e

??
Ty
Abs
-
Dada
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Mar 08, 2010 13:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ajuda] Esboce região de Integração
por sinisterr » Seg Set 22, 2014 00:12
- 0 Respostas
- 815 Exibições
- Última mensagem por sinisterr

Seg Set 22, 2014 00:12
Cálculo: Limites, Derivadas e Integrais
-
- Determine m e n
por Cleyson007 » Qua Mai 20, 2009 13:28
- 4 Respostas
- 5189 Exibições
- Última mensagem por Cleyson007

Sex Mai 29, 2009 10:03
Números Complexos
-
- Determine k
por Cleyson007 » Qui Jun 11, 2009 12:57
- 2 Respostas
- 2321 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 13:19
Polinômios
-
- determine...
por lucianofloripa » Sex Nov 20, 2009 12:38
- 6 Respostas
- 4811 Exibições
- Última mensagem por lucianofloripa

Qui Nov 26, 2009 11:25
Geometria Analítica
-
- Determine MN
por Balanar » Seg Ago 30, 2010 01:36
- 0 Respostas
- 1186 Exibições
- Última mensagem por Balanar

Seg Ago 30, 2010 01:36
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![z=f(x,y)=ln(y-x^2-2x)+\sqrt[2]{2x-x^2-y} z=f(x,y)=ln(y-x^2-2x)+\sqrt[2]{2x-x^2-y}](/latexrender/pictures/88ef5d5b6edb9517e0f77634b547058a.png)
![Df=\left[(x,y)\epsilon\Re^2/y-x^2-2x>0 e 2x-x^2-y\geq0\right] Df=\left[(x,y)\epsilon\Re^2/y-x^2-2x>0 e 2x-x^2-y\geq0\right]](/latexrender/pictures/b95c988ac257bcdceb955863491e4f0a.png) e agora vamos esboçar o gráfico
e agora vamos esboçar o gráfico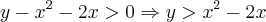 os pontos da parábola onde o gráfico intercepta n deveriam ser
os pontos da parábola onde o gráfico intercepta n deveriam ser  e
e  ??
??
![z=f(x,y)=ln(y-x^2-2x)+\sqrt[2]{2x-x^2-y} z=f(x,y)=ln(y-x^2-2x)+\sqrt[2]{2x-x^2-y}](/latexrender/pictures/88ef5d5b6edb9517e0f77634b547058a.png)
![Df=\left[(x,y)\epsilon\Re^2/y-x^2-2x>0 e 2x-x^2-y\geq0\right] Df=\left[(x,y)\epsilon\Re^2/y-x^2-2x>0 e 2x-x^2-y\geq0\right]](/latexrender/pictures/b95c988ac257bcdceb955863491e4f0a.png) e agora vamos esboçar o gráfico
e agora vamos esboçar o gráfico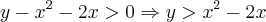 os pontos da parábola onde o gráfico intercepta n deveriam ser
os pontos da parábola onde o gráfico intercepta n deveriam ser  e
e  ??
??

 .
.
 :
: