Bom dia;
considere a função f:[-5,3] ? A, definida por f(x)=|x+2|-3. Se f é sobrejetora então:
a) A=[-6,2]
b) A=[-5,2]
c) A=[-4,2]
d) A=[-3,2]
A reposta correta é a alternativa D. Porém não consigo compreender o cálculo correto para essa resposta, minha dificuldade maior esta na fórmula f(x)=|x+2|-3, Se alguém puder me ajudar?


![[0,2] [0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png) se o domínio é
se o domínio é ![[-5,3] [-5,3]](/latexrender/pictures/117b0133b5e64e3a0d2f85475ed7b728.png)

 -2
-2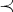 -2
-2 2)
2) [0,2]={-3,-2,-1,0,1,2}=[-3,2]
[0,2]={-3,-2,-1,0,1,2}=[-3,2]

 , avisa que eu resolvo.
, avisa que eu resolvo.

