a)quanto tempo durou a viagem?
b)Qual foi a velocidade média nos primeiros 100km?
Eu fiz da seguinte maneira:100/(x+40)+100/x=200/96,calculei mmc dos denominadores,mas no fim da conta deu números muito altos e me perdi completamente!!!!


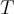 deve ser tal que
deve ser tal que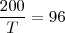 .
.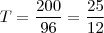 h.
h.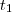 h para percorrer os 100 primeiros kilometros numa velocidade média
h para percorrer os 100 primeiros kilometros numa velocidade média 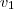 e
e 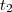 h pra percorrer os outros 100 km numa velocidade média
h pra percorrer os outros 100 km numa velocidade média  , então
, então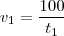 (i)
(i)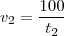 (ii)
(ii)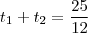 e que (iv)
e que (iv)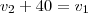 .
.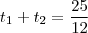
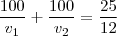
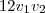 vem que
vem que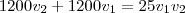 .
.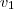 teremos a equação acima transformada em uma equação somente em
teremos a equação acima transformada em uma equação somente em  . Veja:
. Veja: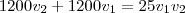
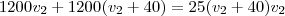
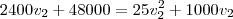
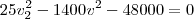
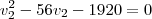
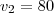 ou
ou 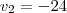 . Já que tratamos a velocidade média como sendo positiva, a 1° solução é a que usaremos.
. Já que tratamos a velocidade média como sendo positiva, a 1° solução é a que usaremos. 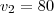 km/h então
km/h então 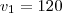 km/h.
km/h.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.