Exemplo: Prove que
 .
.Aí eu poderia fazer (nesse caso aqui assumindo como verdadeira a operação de multiplicação de limites)

Como,
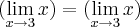
Intuitivamente temos:
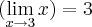
Agora provar isso:
Para todo
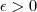 existe um
existe um 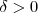 tal que
tal que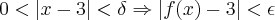
Fazendo nesse caso
 temos que é verdadeiro que
temos que é verdadeiro que 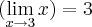
Agora substituindo lá em cima:

3.3=9
9=9 (C.Q.D)
Fica demonstrado, só não sei se é um jeito correto. Alguém pode me dizer se pode ser feito assim ?


 ) existe .
) existe . 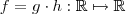 e suponha que demonstramos que os limites
e suponha que demonstramos que os limites 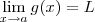 e
e  existem, ou seja , mostramos que
existem, ou seja , mostramos que 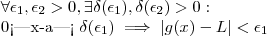
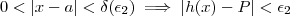 .
. 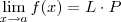 .Isto é, queremos mostrar que dado
.Isto é, queremos mostrar que dado 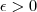 existe
existe 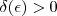 tal que se
tal que se 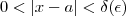 então
então 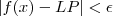 .
.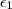 e
e  ) e em seguida obter
) e em seguida obter 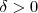 correspondente .
correspondente .  ou
ou  é
é  quando
quando  tende a
tende a  .
. 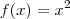 .
.  . Tomando-se
. Tomando-se  , obtemos
, obtemos 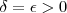 tal que
tal que 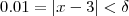 . Mas por outro lado ,
. Mas por outro lado , 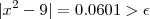 .
. 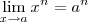 (n natural)
(n natural)
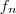 definida pelo monômio
definida pelo monômio  , podemos provar
, podemos provar 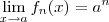 , sem a regra operatória já mencionada.Pq não tentar ? O que acha ?
, sem a regra operatória já mencionada.Pq não tentar ? O que acha ?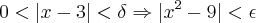
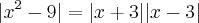

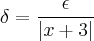
 >0 existe um
>0 existe um  , pondo
, pondo 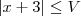 e escolhendo
e escolhendo 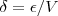 ,teremos
,teremos 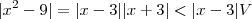 .Daí, se
.Daí, se 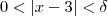 então
então 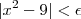 .
. p/ algum
p/ algum  natural . Como provar que
natural . Como provar que 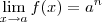 para qq . a real ?? Está tentei fazer , e observei q dado
para qq . a real ?? Está tentei fazer , e observei q dado  , então se
, então se 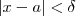 logo
logo 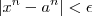 .Quando fazermos
.Quando fazermos  e
e  o delta será igual ao menor valor do conjunto
o delta será igual ao menor valor do conjunto 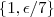 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

