A diferença entre a maior e menor raiz da equação
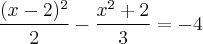
O Gabarito gera a resposta sendo 4.
Grata!


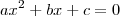 .
.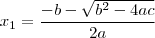 e
e 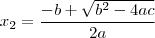 será as raízes da equação .
será as raízes da equação . 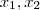 ,ou seja , A diferença entre a maior e menor raiz da equação
,ou seja , A diferença entre a maior e menor raiz da equação 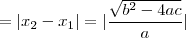 .
.
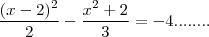
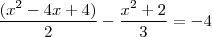 ........
........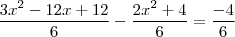 .......
.......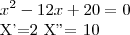

 por
por  . O correto seria multiplicar e dividi o mesmo por
. O correto seria multiplicar e dividi o mesmo por  (assim como você com os outros termos) ,desta forma estaremos multiplicando este número por
(assim como você com os outros termos) ,desta forma estaremos multiplicando este número por  . Partindo da última expressão e trocando
. Partindo da última expressão e trocando 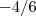 por
por 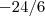 ,segue
,segue 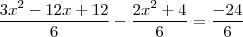 .
. 
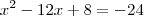 ou ainda
ou ainda 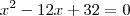
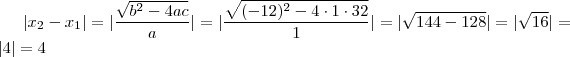 ,
,  e calculando
e calculando  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: