 por mahhfe » Sex Nov 13, 2009 12:10
por mahhfe » Sex Nov 13, 2009 12:10
Estou com dificuldades de resolver essa questão que "aparenta" não ser dificil
UECE 2001.2
Seja N = { 1, 2, 3, 4, ...) e f : A ---> N a função definidade por
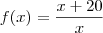
. Se
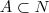
é o dominio mais amplo possível para f, a soma dos 5 menores elementos de A será:
a) 15
b) 18
c) 20
d) 22
Ps. é o meu primeiro post, estou tendo um pouco de dificuldades com os codigos, se algo estiver fora das regras ou codigos errados é só me falarem.
-
mahhfe
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 13, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Nov 13, 2009 13:43
por Molina » Sex Nov 13, 2009 13:43
mahhfe escreveu:Estou com dificuldades de resolver essa questão que "aparenta" não ser dificil
UECE 2001.2
Seja N = { 1, 2, 3, 4, ...) e f : A ---> N a função definidade por
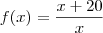
. Se
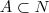
é o dominio mais amplo possível para f, a soma dos 5 menores elementos de A será:
a) 15
b) 18
c) 20
d) 22
Ps. é o meu primeiro post, estou tendo um pouco de dificuldades com os codigos, se algo estiver fora das regras ou codigos errados é só me falarem.
Primeiramente bem-vindo ao fórum! Faça bom uso...
Vamos lá quanto a questão:
Temos a seguinte função
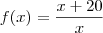
e queremos encontrar valores que quando substituirmos
x em
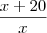
encontremos um número pertencente a N, ou seja, um número natural 1, 2, 3, ...
Não é difícil porque iremos fazer a seguinte "jogada"... Ao invés de usar
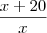
podemos escrever
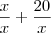
e por consequencia
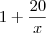
.
Ou seja,
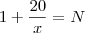
onde N é um número inteiro. Para isso dar inteiro a fração tem que ser redutível, sendo assim temos que encontrar os
x em que vamos dividir 20 e encontrar um número inteiro. Em outras palavras, quais são os 5 primeiros números que 20 é divisível?
Tente resolver agora.
A resposta certa é a letra d)
Qualquer dúvida informe aqui.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por mahhfe » Sex Nov 13, 2009 19:06
por mahhfe » Sex Nov 13, 2009 19:06
Oi Molina, poxa, obrigada!
Consegui! Fiz de duas maneiras inimagináveis e nunca pensei nessa. Sabe com é, estou adentrando no mundo da matemática e aos poucos vou pegando o jeito. O meu problema maior é com a interpretaçao do problema, mas creio que esse é o maior problema da maioria das pessoas.
-
mahhfe
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 13, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5584 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5751 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3490 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2958 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
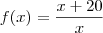 . Se
. Se 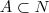 é o dominio mais amplo possível para f, a soma dos 5 menores elementos de A será:
é o dominio mais amplo possível para f, a soma dos 5 menores elementos de A será:

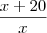 encontremos um número pertencente a N, ou seja, um número natural 1, 2, 3, ...
encontremos um número pertencente a N, ou seja, um número natural 1, 2, 3, ...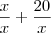 e por consequencia
e por consequencia 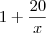 .
.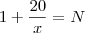 onde N é um número inteiro. Para isso dar inteiro a fração tem que ser redutível, sendo assim temos que encontrar os
onde N é um número inteiro. Para isso dar inteiro a fração tem que ser redutível, sendo assim temos que encontrar os 






