x² - 9
__________
x² - 6x +9
simplificar.
já tentei algumas vezes, mas não me lembro. acho qe da forma qe eu fiz ta certo.
colocando o x² em evidencia, mais queria ter certeza.
por tamirosa » Qui Out 29, 2009 20:11
por Molina » Sex Out 30, 2009 11:37
é a diferença de dois quadrados. Para isso tiramos a raiz quadrada do primeiro termo, ficando com 
e a raiz quadrada do segundo termo, ficando com 
, e escrevemos o seguinte: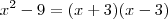
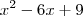é um trinômio do quadrado perfeito, pois se eu tirar a raiz quadrada do primeiro e do último termo e multiplicar por 2 é igual ao termo do meio. Vejamos: Raiz quadrada do primeiro termo é . Raiz quadrada do último termo é . Note que se multiplicarmos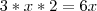 
(que é o termo do meio). Então podemos escrever: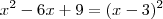
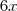ser negativo do lado esquerdo.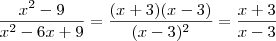
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.