 por brunoafa » Dom Jun 02, 2013 16:56
por brunoafa » Dom Jun 02, 2013 16:56
Em uma apresentação da esquadrilha da fumaça, dois pilotos fizeram manobras em momentos diferentes deixando rastros de fumaça, conforme mostra a figura abaixo.
As funçoes
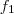
e
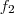
que correspondem às manobras executadas pelos pilotos são
a)
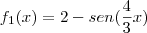
e
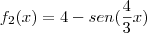
.
b)
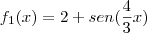
e
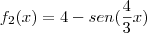
.
c)
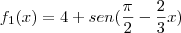
e
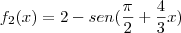
d)
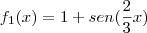
e
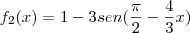
Eu sei que o objetivo do fórum não é somente colar as questões aqui,e eu acho isso intelingente mas a minha dúvida é o seguinte: como achar a função a partir do gráfico?? E outra,esse gráfico não tem correspondente no zero e o primeiro valor já é
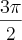
,então eu acho que fica mais difícil...Bom,espero que tenham entendido minha dúvida kkk
-
brunoafa
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 02, 2013 16:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2234 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5463 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- Função composta
por scorpion » Sáb Out 25, 2008 11:09
- 2 Respostas
- 4200 Exibições
- Última mensagem por scorpion

Qua Out 29, 2008 14:26
Funções
-
- Função Composta
 por ginrj » Ter Jun 30, 2009 17:35
por ginrj » Ter Jun 30, 2009 17:35
- 4 Respostas
- 17048 Exibições
- Última mensagem por LuizAquino

Sáb Mar 03, 2012 14:34
Funções
-
- Função composta
 por matemalouco » Sáb Ago 15, 2009 20:43
por matemalouco » Sáb Ago 15, 2009 20:43
- 2 Respostas
- 3983 Exibições
- Última mensagem por Elcioschin

Seg Ago 17, 2009 10:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
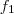 e
e 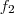 que correspondem às manobras executadas pelos pilotos são
que correspondem às manobras executadas pelos pilotos são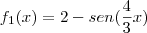 e
e 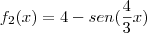 .
.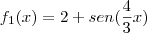 e
e 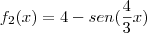 .
.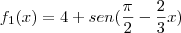 e
e 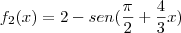
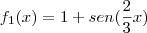 e
e 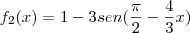
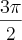 ,então eu acho que fica mais difícil...Bom,espero que tenham entendido minha dúvida kkk
,então eu acho que fica mais difícil...Bom,espero que tenham entendido minha dúvida kkk

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.