Estou resolvendo alguns exercicios de matemática das provas antigas da Fuvest e me deparei com uma situação que não sei mais que caminho seguir.
A questão é a 28 da fuvest 2013, e tem o seguinte enunciado:
---
Sejam
e 
numeros reais com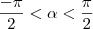 
e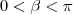 
.Se o sistema de equações, dado em notação matricial,
![\begin{pmatrix}
3 & 6 \\
6 & 8
\end{pmatrix} . \begin{pmatrix}
tg \alpha \\
cos \beta
\end{pmatrix} =
\begin{pmatrix}
0 \\
-2.\sqrt[]{3}
\end{pmatrix}](/latexrender/pictures/6a3c2a6c55cc22b760f01bd3b1c15914.png "\begin{pmatrix}
3 & 6 \\
6 & 8
\end{pmatrix} . \begin{pmatrix}
tg \alpha \\
cos \beta
\end{pmatrix} =
\begin{pmatrix}
0 \\
-2.\sqrt[]{3}
\end{pmatrix}")
for satisfeito, então
é igual a:---
A resposta correta é: -
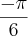
Na minha resolução, eu consegui resolver o sistema tudo certo e cheguei nas seguintes respostas:
tg
= ![- \sqrt[]{3}](/latexrender/pictures/5146764d594e41cc1e0df3c201b01a02.png "- \sqrt[]{3}")
e cos
= ![\frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png "\frac{\sqrt[]{3}}{2}")
A partir daqui eu empaquei na resolução, olhando alguns sites que tem os exercicios resolvidos eles chegam a conclusão qu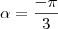e
e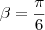 
somente sabendo que um é tangente e outro é coseno e dai fazem a soma.O que eu gostaria de entender é como eles conseguem descobrir os valores de
, e o que eu preciso estudar para ter conhecimento sobre esse assunto. Ja que eu não tenho nem certeza absoluta que isso é um problema para trigonometria.Muito Obrigado!
por 
.
, 
e para 
, 
.
e 
, monte a função e substitua 
por 
.
