a) (
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) ; 2 )
; 2 ) b) (2; 2
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) + 3)
+ 3) c) (-2;
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png) )
) d) (1; 3)
e) (
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) ; - 2
; - 2![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) + 1)
+ 1) Já que a reta s é perpendicular , eu sei que o Coeficiente angular dela se dará por -1/2 . Mas como continuar? Sei também que o raio da circunferência equivale à
![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png) , mas não sei como utilizar esses valores e continuar o problema.
, mas não sei como utilizar esses valores e continuar o problema.

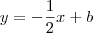


![(\sqrt[]{2}; 2\sqrt[]{2}) (\sqrt[]{2}; 2\sqrt[]{2})](/latexrender/pictures/35245675c5a8961098a0c33d99252cb8.png)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)