 por juannomon » Qua Abr 10, 2013 17:18
por juannomon » Qua Abr 10, 2013 17:18
(Fgv ) Considere a reta r, de equação y = 2x + 3, e a circunferência de equação x² + y² = 10. A reta s, perpendicular à reta r, tangencia a circunferência no ponto P. Esse ponto pode ser
a) (
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
; 2 )
b) (2; 2
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
+ 3)
c) (-2;
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)
)
d) (1; 3)
e) (
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
; - 2
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
+ 1)
Já que a reta s é perpendicular , eu sei que o Coeficiente angular dela se dará por -1/2 . Mas como continuar? Sei também que o raio da circunferência equivale à
![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png)
, mas não sei como utilizar esses valores e continuar o problema.
-
juannomon
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Abr 10, 2013 17:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3º Ano
- Andamento: cursando
 por young_jedi » Qui Abr 11, 2013 15:15
por young_jedi » Qui Abr 11, 2013 15:15
como voce ja tem o coeficiente angular então a equaçao da reta fica
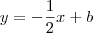
como a reta tangencia a circunferencia então a a distancia da reta ao centro da circunferencia é igual ao raio da mesma
como a circunferencia tem centro em (0,0) calcule a distancia da reta acima ate este ponto e iguale ao raio com isto voce encontrara b e determinara a equação da reta e depois encontre o ponto de tangencia.
Comente qualquer coisa.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por juannomon » Qui Abr 11, 2013 18:26
por juannomon » Qui Abr 11, 2013 18:26
Consegui resolver,muito obrigado

Resposta : letra A ( que por sinal, deveria ser (
![(\sqrt[]{2}; 2\sqrt[]{2}) (\sqrt[]{2}; 2\sqrt[]{2})](/latexrender/pictures/35245675c5a8961098a0c33d99252cb8.png)
-
juannomon
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Abr 10, 2013 17:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3º Ano
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7586 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5261 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
-
- Geometria analítica
por shirata » Qua Nov 11, 2009 20:37
- 2 Respostas
- 4038 Exibições
- Última mensagem por shirata

Dom Nov 15, 2009 09:25
Geometria Espacial
-
- geometria analitica
por Jaison Werner » Sex Abr 23, 2010 21:19
- 3 Respostas
- 3822 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 19:03
Geometria Analítica
-
- geometria analitica
por Jaison Werner » Qui Abr 29, 2010 20:44
- 1 Respostas
- 2690 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 21:10
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) ; 2 )
; 2 ) ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) + 3)
+ 3) ![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png) )
) ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) ; - 2
; - 2![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) + 1)
+ 1) ![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png) , mas não sei como utilizar esses valores e continuar o problema.
, mas não sei como utilizar esses valores e continuar o problema.

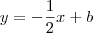


![(\sqrt[]{2}; 2\sqrt[]{2}) (\sqrt[]{2}; 2\sqrt[]{2})](/latexrender/pictures/35245675c5a8961098a0c33d99252cb8.png)
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.