Primeiro comece eliminando os parênteses, ou seja, efetue a multiplicação, então procure isolar o x em lado só da equação, e assim por consequência você terá o valor de x.
Exemplo:

Eliminando os parênteses através da multiplicação:
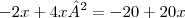
Adicionando "-20x" em ambos os lados da equação:
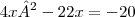
Agora adicionando "20" em ambos os lados da equação:
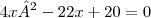
Agora é só achar o valor de x que quando substituído lado direito da equação se igual ao lado esquerdo, ou seja, se torne igual a zero, isso significa encontrar a raíz da equação:
Pela fórmula de bháskara:
![x=\frac{-11+\sqrt[]{31}}{4} x=\frac{-11+\sqrt[]{31}}{4}](/latexrender/pictures/20c3d3d4f4f3b743549c9a25f736e973.png)
![x=\frac{-11-\sqrt[]{31}}{4} x=\frac{-11-\sqrt[]{31}}{4}](/latexrender/pictures/37b9c2ae8557e257585186f13567d80d.png)




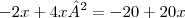
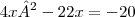
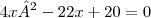
![x=\frac{-11+\sqrt[]{31}}{4} x=\frac{-11+\sqrt[]{31}}{4}](/latexrender/pictures/20c3d3d4f4f3b743549c9a25f736e973.png)
![x=\frac{-11-\sqrt[]{31}}{4} x=\frac{-11-\sqrt[]{31}}{4}](/latexrender/pictures/37b9c2ae8557e257585186f13567d80d.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

