Limite de Sequencia

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Limite de Sequencia

Regras do fórum
Responder

Limite de Sequencia

Mensagempor andrefahl » Qui Out 28, 2010 18:15

Ae galera, sou novo aqui no forum e
to procurando se alguem pode me ajudar com um limite de uma sequencia aqui...

ainda não sei escrever usando o codigo latex, vou aprender e na prox ja boto a formua certinho...
por enquanto vou colocar em uma linha soh...

lim n -> "inf" de (3+((-1)^n)*sqrt(n))/n+2

se alguem puder ajudar agradeço mto ae

vlw!
andrefahl
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 36
Registrado em: Qui Out 28, 2010 18:05
Formação Escolar: GRADUAÇÃO
Área/Curso: Física - UNICAMP
Andamento: cursando
Voltar ao topo

Re: Limite de Sequencia

Mensagempor andrefahl » Qui Out 28, 2010 18:23

Tentando escrever a formula com o LaTex

\lim_{n\to\infty}\frac{3 + (-1)^n\sqrt(n)}{n + 2}

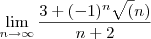
aeeee ateh q consegui =)
andrefahl
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 36
Registrado em: Qui Out 28, 2010 18:05
Formação Escolar: GRADUAÇÃO
Área/Curso: Física - UNICAMP
Andamento: cursando
Voltar ao topo

Re: Limite de Sequencia

Mensagempor andrefahl » Sex Out 29, 2010 13:02

Bom como sou novo aqui no forum não deixei inicialmente qual era a dificuldade,

nesse caso eu não sei o que acontece quando se tem o (-1)^n
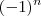
e tambem o problema com a raiz...

por favor ajudem =)
grato!
andrefahl
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 36
Registrado em: Qui Out 28, 2010 18:05
Formação Escolar: GRADUAÇÃO
Área/Curso: Física - UNICAMP
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: cálculo de limites
Autor: Hansegon - Seg Ago 25, 2008 11:29

Bom dia.

Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado

\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]

Assunto: cálculo de limites
Autor: Molina - Seg Ago 25, 2008 13:25

\lim_{x\rightarrow-1} \frac{{x}^{3}+1}{{x}^{2}-1}

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.

Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo. :y:

Caso ainda não tenha dado uma :idea:, avisa que eu resolvo.

Bom estudo!

Assunto: cálculo de limites
Autor: Guill - Dom Abr 08, 2012 16:03

\lim_{x\rightarrow-1}\frac{x^3+1}{x^2-1}

\lim_{x\rightarrow-1}\frac{(x+1)(x^2-x+1)}{(x+1)(x-1)}

\lim_{x\rightarrow-1}\frac{(x^2-x+1)}{(x-1)}=\frac{-3}{2}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum