Gostaria da ajuda de vocês para esta questão aqui...
Tentei mais de uma vez... e nada!
O gabarito não foi modificado... não constava recurso aceito... então... deve haver uma maneira do resultado ser este mesmo... A resposta é D... só consigo achar 10!!
Pra vcx terem uma idéia... fiz até no excel p/ ter certeza de que não estava contando errado. Tentei tb por meio de PA... e nada...
Em um auditório há 30 filas com 24 assentos em cada fila. Os assentos são numerados da esquerda para a direita, começando pela primeira fila. Em que fila está o assento de número 280?
(A) 15 (B) 14 (C) 13 (D) 12 (E) 11
Obrigada!


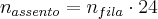
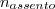 e
e 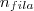 são números inteiros.
são números inteiros.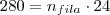
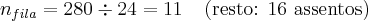
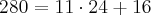

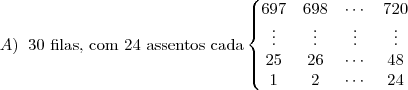
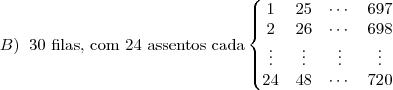
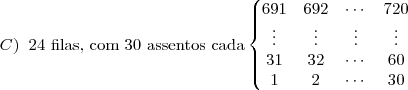
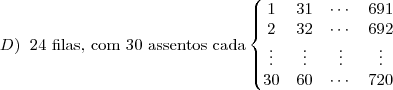
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
