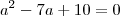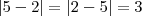por natanskt » Seg Out 11, 2010 16:16
por natanskt » Seg Out 11, 2010 16:16
3-)(ESPCEX) A soma de 2 numeros reais é igual a 7 e a soma dos seus logaritmos na base 100 é 1/2.
o módulo da diferença entre esses dois números é igual a:
a-)0,04
b-)0,02
c-)1
d-)3
e-)2
tambem queria saber o que significa módulo.
valeu !
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Seg Out 11, 2010 17:22
por MarceloFantini » Seg Out 11, 2010 17:22
Vamos interpretar o enunciado:
A soma de dois números reais é 7:
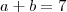 A soma dos seus logaritmos na base 100 é
A soma dos seus logaritmos na base 100 é 
:
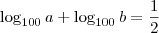
Agora vamos trabalhar com essas informações. A primeira equação não há muito o que fazer, já a segunda pode ser melhorada:
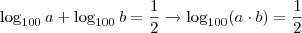
Lembrando a definição de logaritmos (
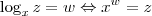
, com as restrições):
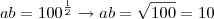
Então temos duas equações:


Primeiro modo:
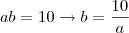
Substituindo na segunda:
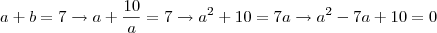
Posso fazer isso pois é certeza que

. Então:
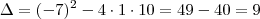
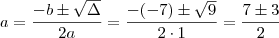
Respostas:

e

ou

e

.
Segundo modo:
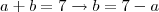
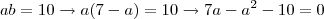
Multiplicando por

:
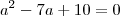
Veja que são meios equivalentes de se chegar na mesma resposta.
Agora entra a importância do módulo.
Módulo quer dizer distância. Módulo entre dois números quer dizer a distância entre eles na reta real. Note que a distância de 5 até 2 é 3, e a distância de 2 até 5 também é 3, porém o que muda é o sentido, simbolizado pelo sinal negativo quando vamos no sentido contrário (ou seja, de 5 para 2). Assim:
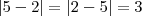
Distância é sempre um número
positivo, ou seja, um
número absoluto.
Alternativa D.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por natanskt » Qua Out 13, 2010 10:20
por natanskt » Qua Out 13, 2010 10:20
fantini,está certo esse jeito que eu fiz....
A+B=7
A.B=10
1+6=7----1.6=6 errado
4+3=7----4.3=12 errado
5+2=7---5.2=10 igual a a.b=10
5-2=3
está certo isso?
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Qua Out 13, 2010 13:50
por MarceloFantini » Qua Out 13, 2010 13:50
Sim, está errado pois não se deve fazer por tentativa e erro, pois é fácil ele colocar uma pegadinha tal que exista uma resposta assim mas que esteja errada. Você tem que entender o que está acontecendo, o porque do método.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:23
- 3 Respostas
- 1763 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:39
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:50
- 2 Respostas
- 5660 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:25
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:53
- 3 Respostas
- 2951 Exibições
- Última mensagem por MarceloFantini

Qui Out 14, 2010 16:38
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Qua Out 13, 2010 18:09
- 2 Respostas
- 4844 Exibições
- Última mensagem por gustavofr

Qui Out 28, 2010 09:19
Logaritmos
-
- (ESPCEX) função logaritmica
por natanskt » Sex Out 29, 2010 10:34
- 1 Respostas
- 1576 Exibições
- Última mensagem por SidneySantos

Qua Abr 20, 2011 20:36
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



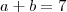
 :
: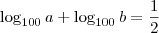
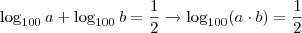
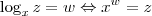 , com as restrições):
, com as restrições):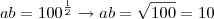


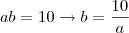
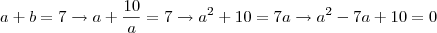
 . Então:
. Então: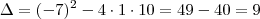
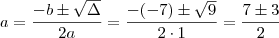
 e
e  ou
ou  e
e  .
.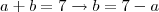
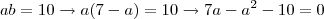
 :
: