 por jose henrique » Ter Out 12, 2010 01:10
por jose henrique » Ter Out 12, 2010 01:10
O maior desastre ecológico produzido pelo homem
está fazendo desaparecer o Mar de Aral, na Ásia, que,
segundo especialistas, estará totalmente seco em 2010.
... Nas últimas quatro décadas, perdeu 60% de sua superfície
e 3/4 do volume de água.
1) Admita que o volume V de água, nesse período, tenha diminuído, a uma taxa anual constante, de
acordo com a função:
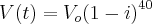
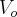
volume há 40 anos
i taxa centesimal anual de diminuição do volume
t tempo medido em anos
tentei resolver assim:
![\frac{3}{4}=1*{\left(1-i \right)}^{40} \Rightarrow \sqrt[40]{\frac{3}{4}}=1-i \Rightarrow 1-\sqrt[40]{\frac{3}{4}}= i \frac{3}{4}=1*{\left(1-i \right)}^{40} \Rightarrow \sqrt[40]{\frac{3}{4}}=1-i \Rightarrow 1-\sqrt[40]{\frac{3}{4}}= i](/latexrender/pictures/260af2112953805e5b8eb9566e8e8a1c.png)
desde já agredeço a atençao!!!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por MarceloFantini » Ter Out 19, 2010 17:20
por MarceloFantini » Ter Out 19, 2010 17:20
Perdeu 60% de sua superfície e 3/4 do seu volume de água, admita equação tal e...o que ele pede? Não compreendi.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jose henrique » Seg Out 25, 2010 21:45
por jose henrique » Seg Out 25, 2010 21:45
oi, desculpa pela demora em responder, mas essa questão foi colocada desta forma e cai num exame adimissional para a uerj. Eu procurar qual o ano caso necessita?
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- resultado diferente da resposta
por natanskt » Seg Dez 06, 2010 13:39
- 1 Respostas
- 2191 Exibições
- Última mensagem por Elcioschin

Seg Dez 06, 2010 14:01
Binômio de Newton
-
- [Integração por frações racionais] Resposta diferente
por rafiusk » Dom Out 07, 2012 00:44
- 5 Respostas
- 2744 Exibições
- Última mensagem por rafiusk

Seg Out 08, 2012 04:16
Cálculo: Limites, Derivadas e Integrais
-
- Adição de Polinômios minha resposta diferente da do livro
por ravi » Ter Jan 31, 2012 14:02
- 2 Respostas
- 2260 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 31, 2012 14:49
Polinômios
-
- resultado diferente - PG
por jose henrique » Qui Set 30, 2010 23:50
- 4 Respostas
- 3217 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 01:18
Progressões
-
- Regra de 3 diferente
por c_zaidan » Qua Dez 08, 2010 17:51
- 2 Respostas
- 3471 Exibições
- Última mensagem por c_zaidan

Qua Dez 08, 2010 19:46
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
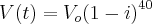
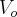 volume há 40 anos
volume há 40 anos ![\frac{3}{4}=1*{\left(1-i \right)}^{40} \Rightarrow \sqrt[40]{\frac{3}{4}}=1-i \Rightarrow 1-\sqrt[40]{\frac{3}{4}}= i \frac{3}{4}=1*{\left(1-i \right)}^{40} \Rightarrow \sqrt[40]{\frac{3}{4}}=1-i \Rightarrow 1-\sqrt[40]{\frac{3}{4}}= i](/latexrender/pictures/260af2112953805e5b8eb9566e8e8a1c.png)



