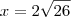por natanskt » Sex Out 08, 2010 12:37
por natanskt » Sex Out 08, 2010 12:37
o conjunto solução da equação

a-)

b-)a-)

c-)

d-)a-)

e-)a-)

-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por natanskt » Sex Out 08, 2010 16:11
por natanskt » Sex Out 08, 2010 16:11
tenho muitos exercicios aqui,tenho uma apostila de um curso preparatorio a distancia,tenho exercicios de matematica,fisica etc...e provas tambem
estou estudando pra entrar na AFA,pega meu msn
natan3tskt@hotmail.comnois converssa lá
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Sex Out 08, 2010 16:41
por DanielRJ » Sex Out 08, 2010 16:41
natanskt escreveu:tenho muitos exercicios aqui,tenho uma apostila de um curso preparatorio a distancia,tenho exercicios de matematica,fisica etc...e provas tambem
estou estudando pra entrar na AFA,pega meu msn
natan3tskt@hotmail.comnois converssa lá
Já add.. mas o meu objetivo é somente matematica eu to muito ruim...
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (AMAN) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:20
- 2 Respostas
- 1391 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 17:13
Logaritmos
-
- (AMAN) inequação logaritmica
por natanskt » Sex Out 29, 2010 10:19
- 0 Respostas
- 915 Exibições
- Última mensagem por natanskt

Sex Out 29, 2010 10:19
Logaritmos
-
- (AMAN) função logaritmica
por natanskt » Sex Out 29, 2010 10:27
- 1 Respostas
- 1539 Exibições
- Última mensagem por DanielFerreira

Qui Nov 18, 2010 17:46
Logaritmos
-
- (ITA) equaçoes logaritmica
por natanskt » Seg Out 11, 2010 17:11
- 6 Respostas
- 4653 Exibições
- Última mensagem por Elcioschin

Qua Out 13, 2010 22:55
Logaritmos
-
- (ITA) equaçoes logaritmica
por natanskt » Qua Out 13, 2010 18:16
- 2 Respostas
- 1368 Exibições
- Última mensagem por MarceloFantini

Sex Out 15, 2010 17:25
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.














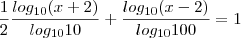
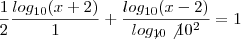
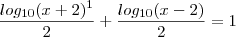
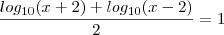
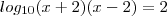

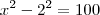
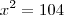
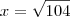
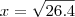
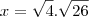
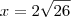
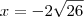
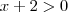 porque é o logaritmano e
porque é o logaritmano e 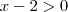 idem.
idem. ---> Ok! e
---> Ok! e  ---Ok!
---Ok!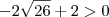 ---> Falso e
---> Falso e 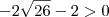 -----> Falso
-----> Falso