 por DanielRJ » Qua Set 29, 2010 17:41
por DanielRJ » Qua Set 29, 2010 17:41
Os lados de um triangulo retangulo estão em p.a. Sabendo-se que o perimetro mede 57 cm, podemos afirmar que o maior cateto mede:
a)17 cm
b)19 cm
c)20 cm
d)23 cm
e)27 cm
Olá pessoal to com um pouco de dificuldade.nesta questão eu só consigo achar B vou mostra minha resolução ai vcs dão um empuranzinho ae.
P.A ---> ( a + b + c)= 57
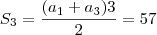
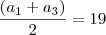
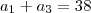
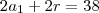
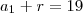 isso aqui será B. por outro lado eu poderia aplicar o Termo medio e achar B denovo. como faço pra achar os outros lados do triangulo?
isso aqui será B. por outro lado eu poderia aplicar o Termo medio e achar B denovo. como faço pra achar os outros lados do triangulo?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Set 29, 2010 20:10
por MarceloFantini » Qua Set 29, 2010 20:10
Fazendo os lados do triângulo
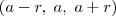
, a soma é

Como é um triângulo retângulo:
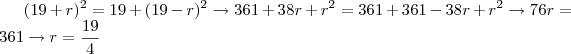
Maior cateto:
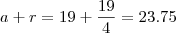
Sobre a outra:
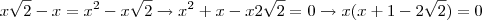
Portanto:

ou
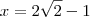
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Qua Set 29, 2010 20:57
por DanielRJ » Qua Set 29, 2010 20:57
Questão puxa mais geometria do que P.A
Obrigado sempre salvando vidas.

-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6607 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- Triangulo
por ginrj » Ter Abr 28, 2009 20:58
- 3 Respostas
- 3794 Exibições
- Última mensagem por ginrj

Sáb Mai 02, 2009 12:30
Geometria Plana
-
- Triângulo.
por Molina » Qua Mai 13, 2009 23:20
- 2 Respostas
- 2155 Exibições
- Última mensagem por Molina

Qui Mai 14, 2009 19:04
Geometria Plana
-
- Triângulo
por cristina » Seg Set 14, 2009 18:49
- 5 Respostas
- 3037 Exibições
- Última mensagem por Marcampucio

Ter Set 15, 2009 16:44
Trigonometria
-
- Triângulo
por Fogodc » Seg Abr 05, 2010 23:39
- 1 Respostas
- 1950 Exibições
- Última mensagem por Fogodc

Qua Abr 07, 2010 11:37
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
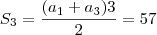
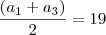
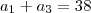
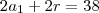
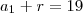



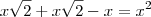
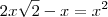
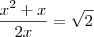
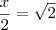
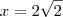 está correto?
está correto?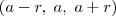 , a soma é
, a soma é 
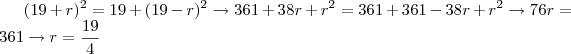
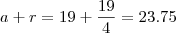
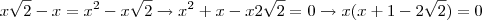
 ou
ou 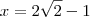




 .
.
 :
: