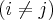 , em quilômetros. Uma empresa estimulou que o custo de transporte por quilômetro para ir da cidade i é dado por C( i, j) = 2i,
, em quilômetros. Uma empresa estimulou que o custo de transporte por quilômetro para ir da cidade i é dado por C( i, j) = 2i,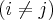 . Segundo essa estimativa, assinale o percurso mais econômico entre os apresentados abaixo:
. Segundo essa estimativa, assinale o percurso mais econômico entre os apresentados abaixo:a) 1
 2
2  3
3b) 1
 3
3  2
2c) 2
 1
1  3
3d) 2
 3
3 1
1e) 3
 1
1  2
2 Achei esta questão muito confusa, ajuda ai galera, pq eu nem sei por onde começa!


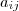 representa o valor do transporte de uma mercadoria saindo de
representa o valor do transporte de uma mercadoria saindo de  e indo até
e indo até 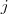 , em outras palavras,
, em outras palavras, 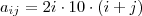 .
.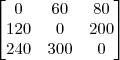
 , o termo é igual a
, o termo é igual a  , afinal, não há distância a ser percorrida para se levar uma mercadoria de 1 até 1, por exemplo
, afinal, não há distância a ser percorrida para se levar uma mercadoria de 1 até 1, por exemplo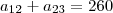 seguindo a lógica...
seguindo a lógica...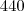
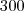
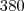
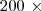
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.