 por DanielRJ » Qui Set 09, 2010 15:43
por DanielRJ » Qui Set 09, 2010 15:43
Uma matriz real A é ortogonal se
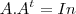
, onde
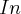
é a matriz identidade e
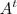
a transposta de A.
Se a Matriz
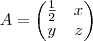
é ortogonal, então

é igual a:
a)1/4
b)1/3
c)1/2
d)3/2
e)2/3
olá pessoal não consigo desenvolver deem uma olh na minha resolução: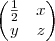
*
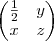
=
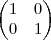
fiz as operações e cheguei a isso:
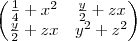
=
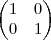 Apartir daqui se estiver correto o que fiz não consigo desenvolver as operações obrigado pessoal até mais.!
Apartir daqui se estiver correto o que fiz não consigo desenvolver as operações obrigado pessoal até mais.!
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Qui Set 09, 2010 17:57
por DanielRJ » Qui Set 09, 2010 17:57
Fantini obrigado pela resposta. Só que fiquei muito confuso nas operações la no final.
tem como explicar sem usar o modulo?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Set 09, 2010 18:26
por MarceloFantini » Qui Set 09, 2010 18:26
O módulo foi apenas questão de rigor. Imaginei que você já soubesse que
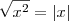
. Ele não altera o resultado final pois, como eu acabei de dizer,
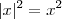
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5165 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3605 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6005 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9699 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12818 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
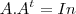 , onde
, onde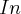 é a matriz identidade e
é a matriz identidade e 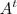 a transposta de A.
a transposta de A.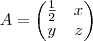 é ortogonal, então
é ortogonal, então é igual a:
é igual a: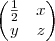 *
* 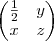 =
=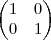 fiz as operações e cheguei a isso:
fiz as operações e cheguei a isso: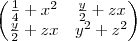 =
=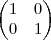


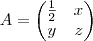
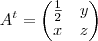
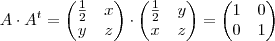
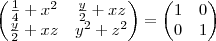
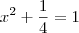
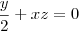
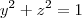
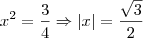
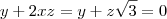
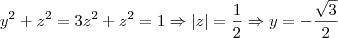
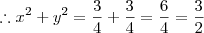


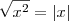 . Ele não altera o resultado final pois, como eu acabei de dizer,
. Ele não altera o resultado final pois, como eu acabei de dizer, 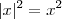 .
.
 .
.



