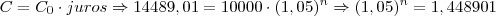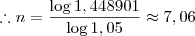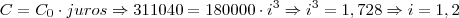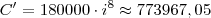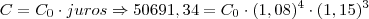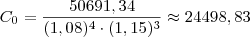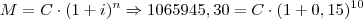O Professor passou uns trinta e pouco exercícios pra gente fazer valendo nota... não consigo fazer esses quatro que ele passou.. =S
Poderiam me ajudar, por favor?
08) Uma pessoa investiu em um banco R$150.000,00, à taxa composta de 10% ao mês, por 4 meses e 10 dias. Qual o montante relativo a essa aplicação?
09) Que taxa mensal de juro composto é recebida por um investidor que aplicam R$ 50.000,00 e resgatou após 8 meses a quantia de R$ 92.546,50?
14) Por quanto tempo deve-se aplicar um capital 10.000,00 à taxa composta de 5% ao mês, para obter-se, no final do prazo, um montante de R$ 14,489,01?
16) Em 1992, depositei R$180.000,00 a juro composto e recebi após 3 meses o valor de R$ 311.040,00. Quanto recebia se estivesse aplicado esse mesmo capital à mesma taxa por 8 meses?
26) Apliquei certa quantia em um banco que me remunerou, nos 4 primeiros meses à taxa composta de 8% ao mês e nos 3 meses seguintes, à taxa composta de 15% ao mês. No final dos sete meses de aplicação, retirei o montante de R$ 50.691,34. Qual era o meu capital inicial?
Tô iniciando no fórum aqui, espero poder dividir minhas dúvidas e até um pouco do meu conhecimento... Desde já muito obrigado, galera!


![C = C_0 \cdot juros \Rightarrow C = 150000 \cdot (1,1)^4 \cdot \sqrt[30]{(1,1)^{10}} \approx 226704,20 C = C_0 \cdot juros \Rightarrow C = 150000 \cdot (1,1)^4 \cdot \sqrt[30]{(1,1)^{10}} \approx 226704,20](/latexrender/pictures/f38b689365bed9068d5396f578c5915a.png)
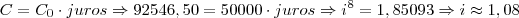 , ou seja, 8%.
, ou seja, 8%.