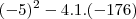(AFA) O numero de arranjos de n+2 objetos tomados 5 a 5 é igual a 180n .Assim, concluirmos que n é um numero:
a) par
b)impar
c)divisivel por 3
d)compreendido entre 10 e 20
bom pessoal tentei bastante essa questão que parece ser facil mais eu travo e não consigo desenvolver então gostaria da ajuda ai do pessoal.abaixo está minha resolução.
minhas tentativas:
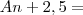
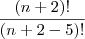diminuindo de (n+2) até (n-3) e simplificando fica assim:
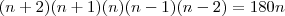passo o N para ----->
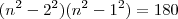
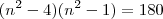nesta parte eu acho que posso passar os numeros para -->>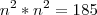
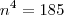
![n=\sqrt[4]{185}](/latexrender/pictures/7d7201649e5e8dfa9fb04317d7fcb338.png "n=\sqrt[4]{185}")
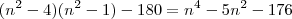
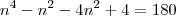
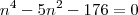
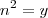temos:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)