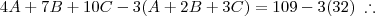por brunotst » Sáb Ago 21, 2010 14:15
por brunotst » Sáb Ago 21, 2010 14:15
Pessoal, estou com uma questão para resolver com base em sistemas lineares e não estou conseguindo, por favor me ajudem.
Uma loja vende três tipos de lâmpada (A, B e C). Ana comprou 4 lâmpadas tipo A, 7 tipo B e 10 tipo C,
pagando R$ 109,00 pela compra. Beto comprou 1 lâmpada tipo A, 2 tipo B e 3 tipo C, o que totalizou R$
32,00. Nas condições apresentadas, quanto custa, nessa loja, a compra de três lâmpadas, sendo uma de
cada tipo?
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por brunotst » Sáb Ago 21, 2010 23:16
por brunotst » Sáb Ago 21, 2010 23:16
Mas quanto custa as três lâmpadas? Você só montou o sistema.
Att.
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Dan » Dom Ago 22, 2010 16:30
por Dan » Dom Ago 22, 2010 16:30
Sim, eu só montei o sistema porque quem vai resolver é você!

Se você já resolveu e encontrou algumas respostas, poste aqui que eu confiro.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por brunotst » Seg Ago 23, 2010 21:18
por brunotst » Seg Ago 23, 2010 21:18
Não estou conseguindo resolver porque tem duas equações e 3 incognitas.
Travei! rsrs
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por brunotst » Ter Ago 24, 2010 20:58
por brunotst » Ter Ago 24, 2010 20:58
Não entendi porque multiplicou a equação por 3? Qual foi o motivo?
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Douglasm » Ter Ago 24, 2010 21:42
por Douglasm » Ter Ago 24, 2010 21:42
Essa foi só uma forma de conseguirmos isolar "A + B + C".
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3092 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4499 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- [SISTEMA] problema que envolve um sistema
por brunnkpol » Qui Jan 02, 2014 22:57
- 2 Respostas
- 2719 Exibições
- Última mensagem por brunnkpol

Seg Jan 06, 2014 21:37
Sistemas de Equações
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5564 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- sistema
por Jessi » Seg Abr 20, 2009 16:56
- 1 Respostas
- 2055 Exibições
- Última mensagem por Marcampucio

Seg Abr 20, 2009 18:08
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


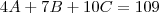

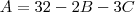 , baseando-se na segunda linha do sistema.
, baseando-se na segunda linha do sistema.