esboçar o gráfico desse polinômio.

[Loretto]

1) Estude a função f(x) = x^4-4x³ com relação aos intervalos de crescimento e decrescimento,com relação à concavidade e pontos de inflexão e esboce o gráfico de f.

Tentei achar a solução da seguinte forma :

1) Domínio : Reais
2) f'(x) = 4x³ - 12 x²
3) f''(x) = 12x² - 24x
4) Estudar ponto de crescimento e decrescimento :

12 x² - 24x = 0
= 4
raízes = 2 e 0

4)


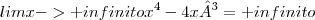
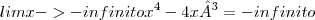
5) Os limites laterais não são necessários de serem calculados, pois a função é contínua em todos os pontos.

f(1) = -4
f(0) = 0
f(2) -32
f(-1) 5

Meu gráfico saiu errado, estou com dúvida pois a f(x) é de grau 4. Como faço esse exercício corretamente ? Obrigado !