 por bilsilva » Sáb Ago 14, 2010 17:52
por bilsilva » Sáb Ago 14, 2010 17:52
Não consigo resolver esse problema:
"Qual é o retângulo máximo inscrito num circulo de raio 12 cm ? "
-
bilsilva
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Ago 14, 2010 17:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Douglasm » Dom Ago 15, 2010 22:35
por Douglasm » Dom Ago 15, 2010 22:35
O que queremos maximizar é a área "S", dada por:
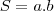
Para podermos verificar o ponto de máximo, devemos primeiro escrever "S" em função de uma variável (nesse caso escolherei "a"). É fácil observar a seguinte relação na circunferência:
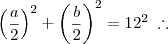
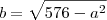
Substituindo em "S":
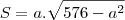
O que temos que fazer agora é encontrar a primeira derivada desta função e igualá-la a zero (posteriormente, a segunda derivada garantirá de que se trata de um ponto de máximo, mas vou omití-la aqui). Logo:
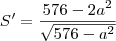
Igualando a zero:
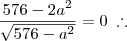
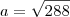
Finalmente, substituindo na relação existente na circunferência, encontramos:
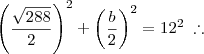
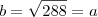
Concluímos que o retângulo com a máxima área a ser inscrito numa circunferência de raio 12 cm é um quadrado de lado

cm.
Obs: Resolvi omitir também o desenvolvimento dos cálculos mas caso haja alguma dúvida nesse sentido é só dizer.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas]- Otimização
por Lucas Monteiro » Seg Jun 25, 2012 18:49
- 2 Respostas
- 2285 Exibições
- Última mensagem por Lucas Monteiro

Ter Jun 26, 2012 17:14
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Uso de otimização
por mikari » Dom Nov 09, 2014 20:01
- 0 Respostas
- 2184 Exibições
- Última mensagem por mikari

Dom Nov 09, 2014 20:01
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas - Otimização
por RafaF2104 » Dom Mar 05, 2017 18:01
- 0 Respostas
- 3146 Exibições
- Última mensagem por RafaF2104

Dom Mar 05, 2017 18:01
Cálculo: Limites, Derivadas e Integrais
-
- [otimização] DERIVADAS PARCIAIS
por montanha » Seg Ago 04, 2008 10:18
- 5 Respostas
- 13113 Exibições
- Última mensagem por admin

Sex Ago 08, 2008 15:14
Cálculo: Limites, Derivadas e Integrais
-
- Problema de otimização - Derivadas
por Napiresilva » Seg Out 10, 2016 15:21
- 1 Respostas
- 3202 Exibições
- Última mensagem por adauto martins

Qui Out 13, 2016 17:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



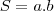
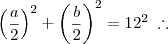
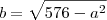
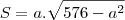
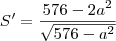
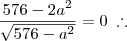
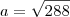
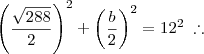
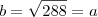
 cm.
cm.