por gutorocher » Qua Jul 21, 2010 21:59
por gutorocher » Qua Jul 21, 2010 21:59
Uma urna contém 6 bolas brancas e 4 bolas vermelhas iguais em tudo menos na cor. Retiramos uma bola, anotamos a cor, recolocamos a bola na urna e retiramos mais uma bola.
a.Qual a probabilidade do resultado ser uma bola vermelha seguida de uma branca ?
6 bolas brancas
4 vermelhas
totalizando = 10 bolas sendo na retirada das bolas tem reposição, conforme mostra no enunciado.
Bola Vermelha:
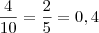
Bola Branca:
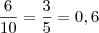
tendo resultado final =
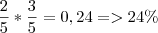
tendo no exercício como resposta : no meu caso deu 24% poderia verificar se o cálculo que fiz está certo, pois não fechou ou é erro do exercício.
a. 10%
b. 12%
c. 18%
d. 36%
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por Tom » Qui Jul 22, 2010 02:01
por Tom » Qui Jul 22, 2010 02:01
Creio que você está correto!
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por gutorocher » Sex Jul 23, 2010 16:10
por gutorocher » Sex Jul 23, 2010 16:10
preciso que mais pessoas verifiquem está questão !
desde já agradeço a todos
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por MarceloFantini » Sáb Jul 24, 2010 01:43
por MarceloFantini » Sáb Jul 24, 2010 01:43
Está certo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gutorocher » Sáb Jul 24, 2010 02:12
por gutorocher » Sáb Jul 24, 2010 02:12
obrigado pela ajuda
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por marcelorenato » Qui Ago 12, 2010 19:09
por marcelorenato » Qui Ago 12, 2010 19:09
Corretíssimo!
-
marcelorenato
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Ago 12, 2010 00:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia e Matemática
- Andamento: formado
 por alexandre32100 » Sex Ago 13, 2010 13:19
por alexandre32100 » Sex Ago 13, 2010 13:19
Perfeito.
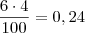
ou
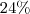
-
alexandre32100
-
 por gutorocher » Sex Ago 13, 2010 15:51
por gutorocher » Sex Ago 13, 2010 15:51
obrigado pelo esclarecimento
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Verificar a Resolução
por eli83 » Ter Out 09, 2012 09:13
- 3 Respostas
- 1860 Exibições
- Última mensagem por eli83

Qua Out 10, 2012 00:39
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Verificar a Resolução I
por eli83 » Ter Out 09, 2012 09:55
- 3 Respostas
- 1735 Exibições
- Última mensagem por eli83

Qua Out 10, 2012 00:31
Cálculo: Limites, Derivadas e Integrais
-
- [verificar a existência] limite trigonométrico
por Fabio Wanderley » Sáb Mar 24, 2012 13:14
- 1 Respostas
- 1491 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 24, 2012 14:49
Cálculo: Limites, Derivadas e Integrais
-
- [Taxa de variação] verificar o desenvolvimento .
por e8group » Sex Jun 01, 2012 20:02
- 3 Respostas
- 5676 Exibições
- Última mensagem por vivik

Qui Mai 17, 2018 05:40
Cálculo: Limites, Derivadas e Integrais
-
- [Equação de planos] Verificar meu raciocínio
por MrJuniorFerr » Qua Out 10, 2012 17:03
- 1 Respostas
- 1236 Exibições
- Última mensagem por young_jedi

Qua Out 10, 2012 19:18
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
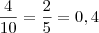
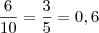
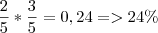






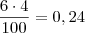 ou
ou