 por engel » Sáb Ago 07, 2010 11:21
por engel » Sáb Ago 07, 2010 11:21
Oi, tenho uma questão da UFRGS que diz assim:
Na igualdade matricial [1 0 0 [1 [1
x 1 0 . 2 = 1
y x 1] 3] 1] o valor de x+y é:
a) -2
b) -1
c) 0
d) 1
e) 2
não está claro nessa visualização, mas ma matriz há um "triângulo de zeros", o que indica que o determinante dela será o produto da diagonal. Então, será 1.
Mas agora, não sei como continuar o cálculo e descobrir quanto vale x+y. Qual o procedimento que devo fazer em igualdades matriciais?
Obrigada!!!!
-
engel
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Dez 30, 2009 16:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Ago 07, 2010 13:50
por Molina » Sáb Ago 07, 2010 13:50
engel escreveu:Oi, tenho uma questão da UFRGS que diz assim:
Na igualdade matricial [1 0 0 [1 [1
x 1 0 . 2 = 1
y x 1] 3] 1] o valor de x+y é:
a) -2
b) -1
c) 0
d) 1
e) 2
não está claro nessa visualização, mas ma matriz há um "triângulo de zeros", o que indica que o determinante dela será o produto da diagonal. Então, será 1.
Mas agora, não sei como continuar o cálculo e descobrir quanto vale x+y. Qual o procedimento que devo fazer em igualdades matriciais?
Obrigada!!!!
Bom dia.
Pelo o que puder ver, o que você quer calcular é:
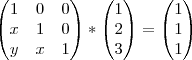
O que você precisa agora é calcular a multiplicação das duas primeiras matrizes. Não há necessidade de relacionar com determinante. Sendo assim...
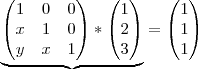
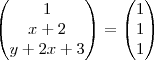
Agora é só igualar os valores:


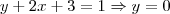
Com isso concluímos que
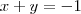
Para próximas questões é indicado que você faça uso do LaTeX (através do Editor de Fórmulas) para melhor visualização da matriz.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação matricial
por SAAMS » Dom Nov 28, 2010 17:18
- 0 Respostas
- 3689 Exibições
- Última mensagem por SAAMS

Dom Nov 28, 2010 17:18
Matrizes e Determinantes
-
- Determine X e Y na igualdade...
por rafaelrosa » Ter Abr 26, 2011 12:57
- 4 Respostas
- 8319 Exibições
- Última mensagem por DanielRJ

Qua Abr 27, 2011 12:08
Matrizes e Determinantes
-
- igualdade de polinomios
por analice » Qui Ago 04, 2011 12:03
- 1 Respostas
- 2186 Exibições
- Última mensagem por Molina

Qui Ago 04, 2011 13:45
Polinômios
-
- Álgebra Matricial
por Claudin » Qui Ago 25, 2011 10:06
- 4 Respostas
- 2254 Exibições
- Última mensagem por Claudin

Sex Ago 26, 2011 01:50
Álgebra Elementar
-
- Matriz Matricial
por ViniRFB » Sex Mar 09, 2012 18:28
- 4 Respostas
- 2960 Exibições
- Última mensagem por ViniRFB

Sex Mar 09, 2012 20:15
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


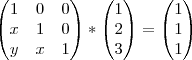
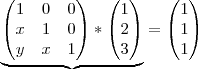
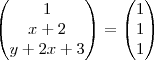


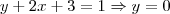
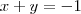


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
