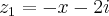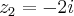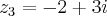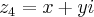, 
, 
, 
, onde x e y são números reais quaisquer e 
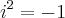. Sobre o conjunto desses números complexos que atendem simultaneamente às condições:I) Re(conjugado de
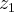. conjugado de 
) 
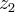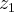Im(conjugado de . conjugado de 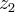)II)
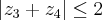
é correto afimar que:
a) representa uma região plana cuja área é menor que 6 unidades de área.
b) possui vários elementos que são números imaginários puros.
c) possui vários elementos que são números reais.
d) seu elemento z de menor módulo possível possui afixo que pertence à reta (r) 3x + 2y = 0
Gabarito: d)
Fazendo as condições I e II, cheguei no seguinte
Condição I)
Condição II)
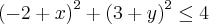
Ou seja, cheguei em um círculo de centro C =(2,-3) e Raio = 2
Fazendo então a representação da interseção de
e do círculo, cheguei em um semi-círculo. A minha dúvida agora é saber se calculei as condições I e II corretamente e analisar cada uma das alternativas. De cara eu achei que a letra B estivesse correta, já que o semi-círculo corresponde a um conjunto de vários números complexos...
Alguém pode resolver para mim? Desde já, agradeço.
Jonatan.
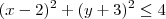
. Como o raio é dois, a área é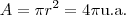 
, que é maior que 6 unidades de área. Se você fizer o gráfico, verá que ele tangencia o eixo y em um ponto e não encosta numa no eixo x, portanto não tem mais de um elemento imaginário puro e não tem nenhum real. A única alternativa que sobra é a D. O menor módulo possível é sempre zero, e a equação de reta que passa pela origem (para caracterizar módulo) e passa pelo centro da circunferência (módulo 0) é a dada na alternativa.
por