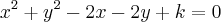passa pelo ponto A(0,1). Sabendo-se que o ponto P pertencente à circunferência mais próximo da origem coincide com o baricentro do triângulo MNQ, onde M(0,k), N(2k,0) e 
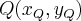é correto afirmar que a área do triângulo MNQ é um número do intervaloGabarito:
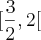
Pessoal, comecei a fazer o seguinte:
1º) Descobri o valor de k = 1, substituindo as coordenadas do ponto k na equação da circunferência dada no início do exercício.
2º) Após isso, achei a seguinte equação da circunferência reduzida:
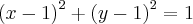
Centro = (1,1) Raio = 1
3º) Achei as coordenadas de M e N, que estavam anteriormente em função de k: M(0,1) e N(2,0)
4º) O exercício falou que o ponto P coincide com o ponto G, que é o baricentro do triângulo MNQ e tal ponto G era pertencente à circunferência e mais próximo da origem. Logo, concluí de que o ponto pertencia a uma reta y = x que passava pela origem e pelo centro (1,1) da circunferência.
5º) Como não tenho as coordenadas do ponto Q, não consigo mais desenvolver o exercício, que acredito eu que para chegarmos ao valor da área devamos fazer uso da fórmula
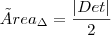
Alguém pode me ajudar? Desde já, agradeço.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.