OLá! sou nova no forum...
Estou quebrando a cabeça pra resolver este exercício de mat que uma criança de 5 anos (ai que vergonha) resolve no 1 dia de aula!Será que alguém pode me ajudar? Sei que aprendi isso... Existe até uma fórmulazinha que relaciona perímetro com área e acho que ela serviria pra resolver ... mas ... quem diz que me lembro!?
Plz, como tenho mttta dificuldade em mat e vcx aqui resolvem questões complexas, podem me mostrar o caminho + fácil pra chegar na resposta?
Obrigada!!
segue o exercício facinho...
O enunciado abaixo refere-se às questões de nos 11 e 12.
Um retângulo tem área igual a 120 dm2. Esse retângulo sofre redução de 20% em sua altura. A fim de que a área do retângulo permaneça inalterada, a base sofre acréscimo.
11
É correto afirmar que esse acréscimo corresponde a
(A) 15%
(B) 20%
(C) 25%
(D) 30%
(E) 35%
12
Considerando-se que a redução na altura corresponda a uma diminuição de 2 dm e que o acréscimo na base corresponda a um aumento de 3 dm, o perímetro desse retângulo antes das alterações em suas medidas correspondia a quantos dm?
(A) 47
(B) 46
(C) 45
(D) 44
(E) 43


 : a medida da altura;
: a medida da altura;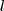 : a medida da base (largura);
: a medida da base (largura);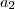 : a medida da altura, após alteração;
: a medida da altura, após alteração;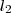 : a medida da largura, após alteração.
: a medida da largura, após alteração.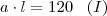
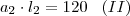
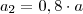
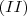 , substituindo
, substituindo 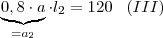
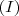 e
e 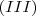 :
: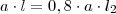

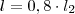
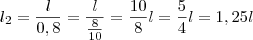
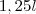 , significa 25% de acréscimo sobre
, significa 25% de acréscimo sobre 
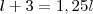
 será (soma dos lados):
será (soma dos lados):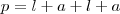
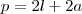


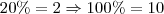 (ou seja, 10 é a altura total do retângulo).
(ou seja, 10 é a altura total do retângulo).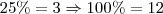 (ou seja, 12 é a largura total do retângulo).
(ou seja, 12 é a largura total do retângulo).




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.