 por gichan » Seg Jul 19, 2010 16:27
por gichan » Seg Jul 19, 2010 16:27
Desculpem, mas eu to com uma dúvida muito básica de números complexos.
Eu sei que essa eh uma das primeiras coisas que se aprende quando se ve essa matéria, mas, mesmo depois de já tê-la visto na escola, essa dúvida ressurgiu depois que meu prof de geometria deu como desafio ver o erro daquelas demonstrações falsas, que 'provam' coisas doidas, tipo 2 = 1, 0 = 1, ou... i² = 1.
Como eu não quero que simplesmente me digam a resposta do problema, queria tirar uma dúvida:
![$\sqrt[2]{-1} *\sqrt[2]{-1}$ $\sqrt[2]{-1} *\sqrt[2]{-1}$](/latexrender/pictures/74f8c1ef74a2bc0f8946bbba0369bd36.png)
é 1 ou -1? E pq?
É que eu pensei de duas formas:
1ª forma:
![$\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$ $\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$](/latexrender/pictures/4b536cf31308587358b59200fc0c32f5.png)
2ª forma:
![$\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$ $\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$](/latexrender/pictures/4921e0da39c6fd936d370c5e36ff0081.png)
Bem, mais uma vez desculpa se for algo muito fácil...
Mas, onde está o erro de algum desses dois raciocinios?
Agradeço desde já ^.^
E peço a compreensão de vcs =D
=* kissú
-

gichan
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Jul 19, 2010 15:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: formado
 por Molina » Seg Jul 19, 2010 19:07
por Molina » Seg Jul 19, 2010 19:07
gichan escreveu:Desculpem, mas eu to com uma dúvida muito básica de números complexos.
Eu sei que essa eh uma das primeiras coisas que se aprende quando se ve essa matéria, mas, mesmo depois de já tê-la visto na escola, essa dúvida ressurgiu depois que meu prof de geometria deu como desafio ver o erro daquelas demonstrações falsas, que 'provam' coisas doidas, tipo 2 = 1, 0 = 1, ou... i² = 1.
Como eu não quero que simplesmente me digam a resposta do problema, queria tirar uma dúvida:
![$\sqrt[2]{-1} *\sqrt[2]{-1}$ $\sqrt[2]{-1} *\sqrt[2]{-1}$](/latexrender/pictures/74f8c1ef74a2bc0f8946bbba0369bd36.png)
é 1 ou -1? E pq?
É que eu pensei de duas formas:
1ª forma:
![$\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$ $\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$](/latexrender/pictures/4b536cf31308587358b59200fc0c32f5.png)
2ª forma:
![$\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$ $\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$](/latexrender/pictures/4921e0da39c6fd936d370c5e36ff0081.png)
Bem, mais uma vez desculpa se for algo muito fácil...
Mas, onde está o erro de algum desses dois raciocinios?
Agradeço desde já ^.^
E peço a compreensão de vcs =D
=* kissú
Buenas!

Essas coisas realmente dão um nó na cabeça.
A maioria das propriedades de raiz quadrada que aprendemos são válidas para todos os números reais positivos, conforme consta
aqui.
Sendo
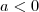
,
![\sqrt[2]{a}*\sqrt[2]{a} \neq \sqrt[2]{a*a} \sqrt[2]{a}*\sqrt[2]{a} \neq \sqrt[2]{a*a}](/latexrender/pictures/f70e9192d518c2f2be6fc04924bb72da.png)
Finalizando,
![\sqrt[2]{-1}*\sqrt[2]{-1} = -1 \sqrt[2]{-1}*\sqrt[2]{-1} = -1](/latexrender/pictures/48c678beedbcdccee78969fb9d0f4be8.png)
Na dúvida o
Google responde, Hehe!


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por gichan » Seg Jul 19, 2010 22:06
por gichan » Seg Jul 19, 2010 22:06
Aháá =P
Não sabia que essa propriedade não servia para os nºs negativos.

Isso me ajudou muito, pq agora eu sei q o erro da prova n tá nessa parte ;D
Anyway, hora de colocar minha mente pra funcionar para achar o erro da prova q i² = 1
=O
Brigadão Diego ^.^
*Nem precisei ir no Google, tá?* uahsuAHSUAsuaHSUAhsuH
Brinks ;D vc foi bem esclarecedor, thank you so much!
=*
-

gichan
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Jul 19, 2010 15:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: formado
 por Molina » Seg Jul 19, 2010 22:13
por Molina » Seg Jul 19, 2010 22:13
gichan escreveu:Aháá =P
Não sabia que essa propriedade não servia para os nºs negativos.

Isso me ajudou muito, pq agora eu sei q o erro da prova n tá nessa parte ;D
Anyway, hora de colocar minha mente pra funcionar para achar o erro da prova q i² = 1
=O
Brigadão Diego ^.^
*Nem precisei ir no Google, tá?* uahsuAHSUAsuaHSUAhsuH
Brinks ;D vc foi bem esclarecedor, thank you so much!
=*
You're welcome!
Não sei se te ajuda onde quer chegar, mas no final do link da wikipedia tem uma demonstração errônea de

, passando por

.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por gichan » Seg Jul 19, 2010 23:35
por gichan » Seg Jul 19, 2010 23:35
O.ops, mais uma mancada minha... eu to malz... =/
Bem, a prova era algo assim:
-1/1 = 1/-1
(I) (II)
(II) (III)
(III) (IV)
(IV)
O erro tá no fato dessa propriedade (edit: de II pra III )não valer para dos nºs negativos, né?
Tipo, se for realmente isso, eu dei uma volta, pq foi exatamente o q vc disse desde o começo e a pessoa distraída aqui não notou que era justamente aí q morava o erro...
Obrigada de novo ^.^
E Boa Noite!
Editado pela última vez por
gichan em Ter Jul 20, 2010 08:12, em um total de 1 vez.
-

gichan
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Jul 19, 2010 15:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: formado
 por Tom » Ter Jul 20, 2010 00:15
por Tom » Ter Jul 20, 2010 00:15
Apenas a nível de informação:
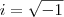
é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por gichan » Ter Jul 20, 2010 08:25
por gichan » Ter Jul 20, 2010 08:25
Tom escreveu:Apenas a nível de informação:
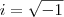
é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.
Mas tomando isso como base, as demais demonstrações podem ser feitas sem problemas, né?
Eu às vezes fico me perguntando como eh q isso entra na cabeça das pessoas tão fácil e eu ainda me enrolo na tal da raiz de menos um =S
Tipo, nas provas, testes, exercícios, eu não me enrolo. Vou bem, por sinal =P
Mas eu n entendi a essência do negócio, se assim poso dizer. Eu aprendi a fazer os exercícios e pronto.
Coisa feia pra quem gosta de mat hehe... Por isso que eu vim aqui ^.^
Meus prof's de mat indicaram O Romance das Equações Algébricas e estou lendo bem confiante de que vai me ajudar =D
Hora de ir pra aula UAHSUahsuAHSUAHSU
valeu again!
E ate mais!
-

gichan
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Jul 19, 2010 15:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: formado
 por Anniinha » Dom Out 31, 2010 02:54
por Anniinha » Dom Out 31, 2010 02:54
a unidade imaginária i = (0,1) por definição.
fazendo i² temos que i.i = (0,1).(0,1)* = (0.0 - 1.1, 0.1 + 1.0) = (-1,0) = -1
ou seja, i² = -1 ou
![i = \sqrt[]{-1} i = \sqrt[]{-1}](/latexrender/pictures/b2d69e603f696fdfb9e3f4c879ddb134.png)
*Multiplicação de um numero complexo:
de

e

:
temos que

-

Anniinha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Out 31, 2010 01:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Geofísica
- Andamento: cursando
 por gichan » Dom Out 31, 2010 18:50
por gichan » Dom Out 31, 2010 18:50
Anniinha escreveu:*Multiplicação de um numero complexo:
de

e

:
temos que

A multiplicação de um numero complexo tbm é por definição, Ana?
-

gichan
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Seg Jul 19, 2010 15:33
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Programação
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- conjuntos do triplo menos 1
por hevhoram » Seg Mai 23, 2011 12:11
- 1 Respostas
- 1959 Exibições
- Última mensagem por Molina

Seg Mai 23, 2011 12:28
Conjuntos
-
- Inequação - Multiplicação por menos um
por Davi Wesley » Sex Set 05, 2014 21:24
- 1 Respostas
- 2853 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:03
Inequações
-
- Como calcular tangente a menos 1
por macburn » Seg Abr 11, 2011 22:07
- 8 Respostas
- 25008 Exibições
- Última mensagem por Marcio Barbosa

Seg Jul 31, 2017 22:05
Trigonometria
-
- NÚMEROS INTEIROS,erros para menos
por Valmel » Qui Out 24, 2013 15:04
- 0 Respostas
- 1043 Exibições
- Última mensagem por Valmel

Qui Out 24, 2013 15:04
Aritmética
-
- [Limites]Tendendo a mais e a menos infinito
por Brunorp » Sex Abr 03, 2015 12:42
- 1 Respostas
- 1504 Exibições
- Última mensagem por adauto martins

Sex Abr 03, 2015 21:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![$\sqrt[2]{-1} *\sqrt[2]{-1}$ $\sqrt[2]{-1} *\sqrt[2]{-1}$](/latexrender/pictures/74f8c1ef74a2bc0f8946bbba0369bd36.png) é 1 ou -1? E pq?
é 1 ou -1? E pq?![$\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$ $\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$](/latexrender/pictures/4b536cf31308587358b59200fc0c32f5.png)
![$\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$ $\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$](/latexrender/pictures/4921e0da39c6fd936d370c5e36ff0081.png)



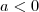 ,
, ![\sqrt[2]{a}*\sqrt[2]{a} \neq \sqrt[2]{a*a} \sqrt[2]{a}*\sqrt[2]{a} \neq \sqrt[2]{a*a}](/latexrender/pictures/f70e9192d518c2f2be6fc04924bb72da.png)
![\sqrt[2]{-1}*\sqrt[2]{-1} = -1 \sqrt[2]{-1}*\sqrt[2]{-1} = -1](/latexrender/pictures/48c678beedbcdccee78969fb9d0f4be8.png)



 , passando por
, passando por  .
.


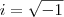 é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.
é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.
![i = \sqrt[]{-1} i = \sqrt[]{-1}](/latexrender/pictures/b2d69e603f696fdfb9e3f4c879ddb134.png)
 e
e  :
:


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.