 por PeIdInHu » Ter Jul 20, 2010 02:45
por PeIdInHu » Ter Jul 20, 2010 02:45
Alguem pode me ajudar estou com duvida nesses dois exercicios....
Utilizando Teorema do confronto mostre que:
i)
![\lim_{x\rightarrow3} g(x).\left[x \right] = 0 \lim_{x\rightarrow3} g(x).\left[x \right] = 0](/latexrender/pictures/5c2e7d51dec1a333a75a8a60de5c0ae9.png)
onde [x] (funçao maior inteiro menor que x) e
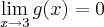
ii)
![\lim_{x\rightarrow\infty} \frac{x - [x]}{x}= 0 \lim_{x\rightarrow\infty} \frac{x - [x]}{x}= 0](/latexrender/pictures/bb1bfd45f67bbe252d911bbaae206d27.png)
-
PeIdInHu
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 22, 2010 14:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Imformatica Biomedica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema do Confronto
por Claudin » Qua Mai 25, 2011 19:51
- 3 Respostas
- 3442 Exibições
- Última mensagem por LuizAquino

Qua Mai 25, 2011 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do Confronto
por Cleyson007 » Seg Jul 11, 2011 22:02
- 3 Respostas
- 2441 Exibições
- Última mensagem por MarceloFantini

Ter Jul 12, 2011 09:05
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do confronto
por jemourafer » Dom Abr 01, 2012 20:23
- 1 Respostas
- 1679 Exibições
- Última mensagem por NMiguel

Dom Abr 01, 2012 21:00
Cálculo: Limites, Derivadas e Integrais
-
- [limite]teorema do confronto
por gabriel feron » Dom Mai 06, 2012 20:25
- 1 Respostas
- 1823 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 22:53
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES - Teorema do confronto
por paola-carneiro » Dom Jun 03, 2012 20:53
- 1 Respostas
- 1911 Exibições
- Última mensagem por Fabio Wanderley

Seg Jun 04, 2012 02:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow3} g(x).\left[x \right] = 0 \lim_{x\rightarrow3} g(x).\left[x \right] = 0](/latexrender/pictures/5c2e7d51dec1a333a75a8a60de5c0ae9.png)
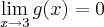
![\lim_{x\rightarrow\infty} \frac{x - [x]}{x}= 0 \lim_{x\rightarrow\infty} \frac{x - [x]}{x}= 0](/latexrender/pictures/bb1bfd45f67bbe252d911bbaae206d27.png)

![\lim_{x\rightarrow3} g(x).\left[x \right] = 0 \lim_{x\rightarrow3} g(x).\left[x \right] = 0](/latexrender/pictures/5c2e7d51dec1a333a75a8a60de5c0ae9.png)
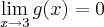
![\lim_{x\rightarrow\infty} \frac{x - [x]}{x}= 0 \lim_{x\rightarrow\infty} \frac{x - [x]}{x}= 0](/latexrender/pictures/bb1bfd45f67bbe252d911bbaae206d27.png)
