Construa,usando o sistema cartesiano ortogonal,os gráficos das funções definidas por:
a)f(x)={2x,se x>=0
-1,se x<0
b)f(x)={3,se x<=0
-x+3,se x>0



Luiza Pamela escreveu:Construa,usando o sistema cartesiano ortogonal,os gráficos das funções definidas por:
a)f(x)={2x,se x>=0
-1,se x<0
b)f(x)={3,se x<=0
-x+3,se x>0
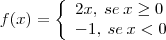
 . Construir essa reta você sabe, correto? Um dos modos mais simples é dar valores a x e descobrir o valor de y. Basta dois valores, por exemplo:
. Construir essa reta você sabe, correto? Um dos modos mais simples é dar valores a x e descobrir o valor de y. Basta dois valores, por exemplo: 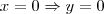 e quando
e quando 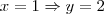
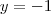 , que é uma constante. Fazer esta reta é mais simples ainda, pois qualquer valor que eu assumir em x, y valerá -1. Dúvidas?
, que é uma constante. Fazer esta reta é mais simples ainda, pois qualquer valor que eu assumir em x, y valerá -1. Dúvidas?
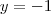


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

