 por rafael84 » Ter Jul 13, 2010 22:58
por rafael84 » Ter Jul 13, 2010 22:58
Um capital é aplicado por doze anos e seis meses a juros compostos de meio por cento ao mês .
Ao final desse período , o rendimento acumulado será igual , inferior ou superior a 100 % ?
Justtifique sua resposta
-
rafael84
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jul 13, 2010 22:48
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Qua Jul 14, 2010 01:42
por MarceloFantini » Qua Jul 14, 2010 01:42
Doze anos e seis meses são 150 meses. Logo, o capital será:
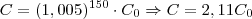
. Assim, o rendimento foi de 111%.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por andersonusa2003 » Sex Out 22, 2010 13:38
por andersonusa2003 » Sex Out 22, 2010 13:38
Pegaremos um exemplo ...
1.000,00 CHS PV
0,5 = i
150 = n
teremos os 1.000,00 corrigidos a juros compostos .. R$ 2.113,05 ... logo o rendiemento foi de R$ 1.113,05 .... superio a 100% ...
-
andersonusa2003
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Out 22, 2010 13:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UFRJ 2009 ) Questão do vestibular da ufrj em 2009 me ajudem
por rafael84 » Ter Jul 13, 2010 22:57
- 1 Respostas
- 2592 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 15, 2010 01:28
Binômio de Newton
-
- Retirada de salário daqui a 8 anos?
por Akemi Miada » Qui Nov 26, 2015 22:32
- 0 Respostas
- 1307 Exibições
- Última mensagem por Akemi Miada

Qui Nov 26, 2015 22:32
Matemática Financeira
-
- Valor aplicado
por marinalcd » Sáb Mar 19, 2016 21:12
- 0 Respostas
- 1209 Exibições
- Última mensagem por marinalcd

Sáb Mar 19, 2016 21:12
Matemática Financeira
-
- Dúvida Eq. Diferenciais 2ª Ordem - Ex. Aplicado
por daniel2678 » Qua Abr 27, 2011 02:14
- 2 Respostas
- 3234 Exibições
- Última mensagem por 0146251

Seg Mai 25, 2015 21:42
Cálculo: Limites, Derivadas e Integrais
-
- Funções Quadráticas aplicado a Agronomia
por ronald_lima » Qui Jun 16, 2016 22:12
- 0 Respostas
- 2484 Exibições
- Última mensagem por ronald_lima

Qui Jun 16, 2016 22:12
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



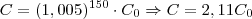 . Assim, o rendimento foi de 111%.
. Assim, o rendimento foi de 111%.


