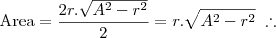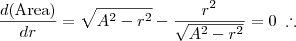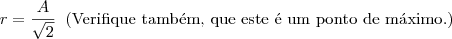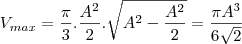por Herrero088 » Seg Jul 12, 2010 23:31
por Herrero088 » Seg Jul 12, 2010 23:31
Bom estou com uma duvida enorme!! estou com uma lista e exercicio e acabei me deparando com um exercicio a meu ver complicado
vamos a ele
"Para construir uma taça em forma de cone circular reto, remove-se um setor de uma folha circular de cartolina de raio A, e unem-se as duas margens retilineas de corte. determine o volume da maior taça que pode ser construida.

tentativa resolução:
se o raio da cartolina é A
então 2?r=A ou r=A/(2?)
bom.. agradeço desde já quem poder me ajudar!!
-
Herrero088
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jul 12, 2010 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. de produção
- Andamento: cursando
 por Elcioschin » Ter Jul 13, 2010 19:10
por Elcioschin » Ter Jul 13, 2010 19:10
Sejam:
x (em radianos) o ângulo do setor circular retirado
S o comprimento da parte curva da figura:
R o raio da base do cone
h a altura do cone
S = 2*pi*A - A*x ----> Este comprimento S será o perimetro da base do cone ----> S = 2*pi*R
2*pi*R = 2*pi*A - A*x ----> R = A - (A/2*pi)*x ----> R² = A² - (A²/pi)*x + (A²/4*pi²)*x²
A dimensão A será a geratriz do cone ----> h² = A² - R² ----> h = V[(A²/pi)*x - (A²/4*pi²)*x²]
V = (1/3)*pi*R²*h -----> V= (1/3)*pi*[A² - (A²/pi)*x + (A²/4*pi²)*x²]*V[(A²/pi)*x - (A²/4*pi²)*x²]
Agora é contigo: Derive, iguale a derivada a zero e calcule x.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Douglasm » Ter Jul 13, 2010 19:47
por Douglasm » Ter Jul 13, 2010 19:47
Eu fiz de um modo diferente do Elcioschin, mas que acredito também ser válido. O problema envolve descobrir um ponto de máximo na função que determina o volume do cone. Para simplificar, ao invés de considerar esta, eu resolvi considerar a função que determina a área do triângulo cuja rotação dá origem ao cone. É evidente que se este triângulo tiver área máxima, o cone terá volume máximo. Eis um desenho do triângulo:
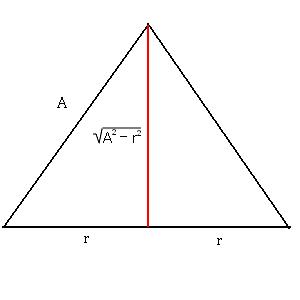
- trimatder.JPG (6.72 KiB) Exibido 2687 vezes
A área do triângulo é dada por:
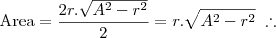
Agora devemos igualar a derivada a zero para encontrarmos um ponto de máximo (ou de mínimo, ou de inflexão):
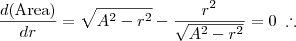
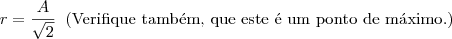
Achamos então, qual deve ser o raio, caso queiramos a área máxima. Este valor também é válido para o volume máximo. Logo:
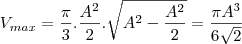
É sempre bom verificar o gabarito, para garantir que não tenhamos errado nas contas. Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema com Derivada
por veldri » Qua Jun 02, 2010 13:51
- 0 Respostas
- 1066 Exibições
- Última mensagem por veldri

Qua Jun 02, 2010 13:51
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Problema
por iceman » Dom Set 16, 2012 20:05
- 3 Respostas
- 1732 Exibições
- Última mensagem por Renato_RJ

Dom Set 16, 2012 20:49
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Problema [2]
por iceman » Dom Set 16, 2012 21:07
- 6 Respostas
- 2683 Exibições
- Última mensagem por iceman

Dom Set 16, 2012 22:15
Cálculo: Limites, Derivadas e Integrais
-
- Problema com resolução da derivada de uma função
por DavidUserCalc » Qua Mar 31, 2010 19:50
- 2 Respostas
- 3196 Exibições
- Última mensagem por DavidUserCalc

Qui Abr 01, 2010 01:19
Cálculo: Limites, Derivadas e Integrais
-
- Problema com a derivada de uma função composta
por DavidUserCalc » Qui Abr 01, 2010 14:44
- 1 Respostas
- 1956 Exibições
- Última mensagem por Molina

Qui Abr 01, 2010 16:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.