 por lcepej » Sex Jul 09, 2010 21:46
por lcepej » Sex Jul 09, 2010 21:46
-
lcepej
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Jul 09, 2010 20:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em informática
- Andamento: cursando
 por PeIdInHu » Sex Jul 09, 2010 23:56
por PeIdInHu » Sex Jul 09, 2010 23:56
vou tentar dar minha contribuiçao..
nao sei se esta certo...se estiver errado alguem me corrija
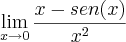
<=> 0/0 <=> L´Hopital
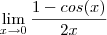
<=> 0/0 <=>aplica novamente L´Hopital
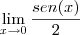
= 0 (ps:nao é certeza kkk)
---------------------------------------------------------------------------------------------
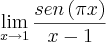
<=> 0/0 <=>L´Hopital
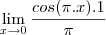
=
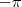
(ps:nao é certeza kkk)
-----------------------------------------------------------------------------------------------------
Editado pela última vez por
PeIdInHu em Sáb Jul 10, 2010 14:23, em um total de 2 vezes.
-
PeIdInHu
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 22, 2010 14:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Imformatica Biomedica
- Andamento: cursando
 por Tom » Sáb Jul 10, 2010 03:45
por Tom » Sáb Jul 10, 2010 03:45
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por PeIdInHu » Sáb Jul 10, 2010 22:02
por PeIdInHu » Sáb Jul 10, 2010 22:02
![\lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3 \lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3](/latexrender/pictures/b67ab103c6ea795e07a3bec4eab14eda.png)
faltou a raiz cubica...?
-
PeIdInHu
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 22, 2010 14:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Imformatica Biomedica
- Andamento: cursando
 por Tom » Sáb Jul 10, 2010 23:28
por Tom » Sáb Jul 10, 2010 23:28
PeIdInHu escreveu:![\lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3 \lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3](/latexrender/pictures/b67ab103c6ea795e07a3bec4eab14eda.png)
faltou a raiz cubica...?
Desculpe, não vi. Nesse caso a resposta é
![\sqrt[3]{3} \sqrt[3]{3}](/latexrender/pictures/00183145853114fdd8d947a663084fb6.png)
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] duvidas.
 por princeandrews » Qui Set 28, 2017 03:37
por princeandrews » Qui Set 28, 2017 03:37
- 0 Respostas
- 3160 Exibições
- Última mensagem por princeandrews

Qui Set 28, 2017 03:37
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas em Limites e derivadas
por babiiimbaa » Dom Ago 29, 2010 20:02
- 0 Respostas
- 1396 Exibições
- Última mensagem por babiiimbaa

Dom Ago 29, 2010 20:02
Cálculo: Limites, Derivadas e Integrais
-
- Dúvidas e curiosidade com os limites fundamentais
por Luthius » Seg Ago 03, 2009 11:29
- 4 Respostas
- 4234 Exibições
- Última mensagem por Luthius

Ter Ago 04, 2009 08:44
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvidas no exercício. Me ajude na Resolução.
 por Thamiires » Ter Nov 29, 2011 21:18
por Thamiires » Ter Nov 29, 2011 21:18
- 1 Respostas
- 1670 Exibições
- Última mensagem por TheoFerraz

Ter Nov 29, 2011 22:30
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5411 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
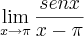
![\lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}} \lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}](/latexrender/pictures/19f8eaf9d333444e9f5a3ec2e05c5458.png)
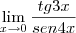
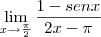
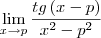
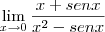
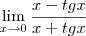
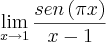
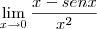

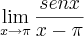
![\lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}} \lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}](/latexrender/pictures/19f8eaf9d333444e9f5a3ec2e05c5458.png)
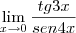
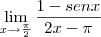
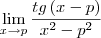
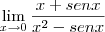
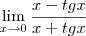
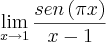
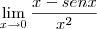

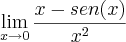 <=> 0/0 <=> L´Hopital
<=> 0/0 <=> L´Hopital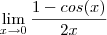 <=> 0/0 <=>aplica novamente L´Hopital
<=> 0/0 <=>aplica novamente L´Hopital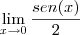 = 0 (ps:nao é certeza kkk)
= 0 (ps:nao é certeza kkk)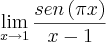 <=> 0/0 <=>L´Hopital
<=> 0/0 <=>L´Hopital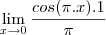 =
= 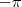

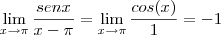 , pela aplicação do Teorema de L'Hospital.
, pela aplicação do Teorema de L'Hospital.![\lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3 \lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3](/latexrender/pictures/b67ab103c6ea795e07a3bec4eab14eda.png)
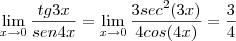
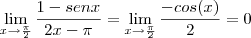
![\lim_{x\rightarrow p} \frac{tg \left(x - p\right)}{x^2 - p^2}=\lim_{x\rightarrow p} \frac{sen\left(x - p\right)}{cos(x-p)[x-p][x+p]} \lim_{x\rightarrow p} \frac{tg \left(x - p\right)}{x^2 - p^2}=\lim_{x\rightarrow p} \frac{sen\left(x - p\right)}{cos(x-p)[x-p][x+p]}](/latexrender/pictures/c46d28ead199ceb4b8a24fcb3ed64bdc.png) e mediante aplicação do limite fundamental entre seno e o arco, decorre:
e mediante aplicação do limite fundamental entre seno e o arco, decorre: ![\lim_{x\rightarrow p} \frac{1}{cos(x-p)[x+p]}=\frac{1}{2p} \lim_{x\rightarrow p} \frac{1}{cos(x-p)[x+p]}=\frac{1}{2p}](/latexrender/pictures/1e8c7e0d30bab85f15ced19f9d26398b.png)
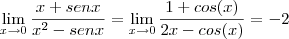
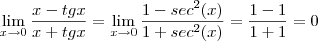
![\lim_{x\rightarrow1} \frac{sen \left(\pi x \right)}{x-1}=\lim_{x\rightarrow1} \frac{\pi[cos(\pi x)]}{1}=-\pi \lim_{x\rightarrow1} \frac{sen \left(\pi x \right)}{x-1}=\lim_{x\rightarrow1} \frac{\pi[cos(\pi x)]}{1}=-\pi](/latexrender/pictures/8e7c5a5db08df8134205ce6ffd35d95c.png)
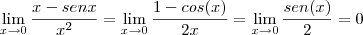

![\lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3 \lim_{x \rightarrow-1} \sqrt[3]{\frac{x^3 + 1}{x + 1}}=\lim_{x \rightarrow-1} \sqrt[3]{\frac{(x+1)(x^2-x+1)}{x + 1}}=\lim_{x\rightarrow -1} x^2-x+1=3](/latexrender/pictures/b67ab103c6ea795e07a3bec4eab14eda.png) faltou a raiz cubica...?
faltou a raiz cubica...?
faltou a raiz cubica...?
![\sqrt[3]{3} \sqrt[3]{3}](/latexrender/pictures/00183145853114fdd8d947a663084fb6.png)
