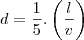Essa é uma questão que envolve a regra de 3 composta. Sugiro que você estude
proporcionalidade e
regra de 3 para conseguir resolvê-la, pois não será nada fácil de você entender a minha explicação se suas noções não forem muito boas nesses conteúdos.
Iniciamos fazendo uma análise da proporcionalidade das grandezas envolvidas no problema. Devemos pensar da seguinte maneira: quanto mais quilômetros devem ser rodados, mais dias levará. Quanto menos velocidade empregada, mais dias levará. Assim, podemos perceber que a quantidade de quilômetros e dias são
diretamente proporcionais (pois quando um aumenta, o outro aumenta) e que a velocidade e os dias são
inversamente proporcionais (pois quando um diminui, o outro aumenta e vice e versa).
Todas essas grandezas devem ser submetidas a uma constante de proporcionalidade, que será indicada por "k". A velocidade em quilômetros é "v", a quantidade de quilômetros será "l" e a quantidade de dias será "d":
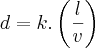
Perceba que a grandeza diretamente proporcional aos dias, que é a quantidade de quilômetros, está no numerador. E a grandeza inversamente proporcional, que é a velocidade, está no denominador. Isso se deve justamente à questão da proporcionalidade.
A partir desta equação, nós aplicamos os dados que conhecemos para descobrir a constante de proporcionalidade:
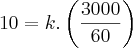
Fazendo as devidas manipulações algébricas, chegaremos à conclusão de que
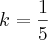
.
Esta é a constante de proporcionalidade, que você deve substituir na equação, para deixá-la completa:
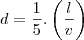
Aí você pode substituir qualquer distância l e qualquer velocidade v para determinar a quantidade de dias.
No caso do seu exercício, a resposta será 18 dias.
Dúvidas, comente.


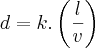
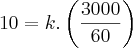
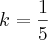 .
.