Um poliedro convexo tem 5 faces quadrangulares e 4 faces triangulares. O número de diagonais é:
a) 6
b) 8
c) 9
d) 10
e) 12



 (pois cada um dos 5 quadrados possui 4 arestas e cada um dos 4 triângulos possui 3 arestas)
(pois cada um dos 5 quadrados possui 4 arestas e cada um dos 4 triângulos possui 3 arestas)
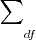 : Somatória das diagonais das faces
: Somatória das diagonais das faces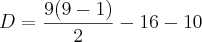
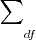 , basta utilizar a fórmula da diagonal para figuras planas
, basta utilizar a fórmula da diagonal para figuras planas 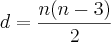 , para cada figura geométrica, no caso apenas o quadrado possui diagonal, e cada quadrado possui 2 diagonais.
, para cada figura geométrica, no caso apenas o quadrado possui diagonal, e cada quadrado possui 2 diagonais.
Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes