 por hevhoram » Qui Jun 24, 2010 11:56
por hevhoram » Qui Jun 24, 2010 11:56
sabemos que o cquociente de dois numeros irracionais pode ser um numero racional. Das alternativas abaixo, qual exemplifica essa afirmação?
a)
![\frac{\sqrt[]{2}}{\sqrt[]{4}}= \frac{1}{\sqrt[]{2}} \frac{\sqrt[]{2}}{\sqrt[]{4}}= \frac{1}{\sqrt[]{2}}](/latexrender/pictures/d3e726b6485fda7dd3b31f9ebfd962cc.png)
b)
![\frac{\sqrt[]{2}}{\sqrt[]{18}} = \frac{1}{\sqrt[]{9}} \frac{\sqrt[]{2}}{\sqrt[]{18}} = \frac{1}{\sqrt[]{9}}](/latexrender/pictures/244daba5ed16488e2e3dd603ace81888.png)
c)
![\frac{\sqrt[]{16}}{\sqrt[]{36}} = \frac{2}{3} \frac{\sqrt[]{16}}{\sqrt[]{36}} = \frac{2}{3}](/latexrender/pictures/5bfa919ddf41a87177fd1580a73f06db.png)
d)
![\frac{\sqrt[]{2}}{\sqrt[]{36}} = \frac{2}{6 \sqrt[]{2}} \frac{\sqrt[]{2}}{\sqrt[]{36}} = \frac{2}{6 \sqrt[]{2}}](/latexrender/pictures/a5ed910fefef5d9508f6763472c433f5.png)
e)
![\frac{\sqrt[]{2}}{\sqrt[]{20}} = \frac{1}{\sqrt[]{10}} \frac{\sqrt[]{2}}{\sqrt[]{20}} = \frac{1}{\sqrt[]{10}}](/latexrender/pictures/37dc80f8b2d39ef5b8008b2553257adb.png)
eu enviei antes só com duas alternativas mais ainda nao entendi a questão: pelo que eu entendi era para fazer meios por extremos mas a resposta do forum pelo meu entendimento foi que a segunda fração já seria o resultado??? mais ai ia ficar mais confuso ainda, pois já tem a letra "c" que no segundo membro é 2/3 nao entendi por fazvor me socoorram!!!
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por Douglasm » Qui Jun 24, 2010 12:47
por Douglasm » Qui Jun 24, 2010 12:47
Olá hevhoram. Se você observar as opções verá que somente as alternativas
b e
c apresentam números racionais como resultado. Mas veja que o enunciado fala da divisão de 2 números
irracionais. Na alternativa
c temos:
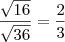
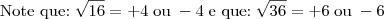
Ou seja, ambos são números
racionais. Sendo assim, a alternativa correta é a letra
b.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Jun 24, 2010 14:03
por MarceloFantini » Qui Jun 24, 2010 14:03
Douglas,
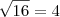
e
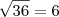
, obrigatoriamente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Números Irracionais] Soma de irracionais dando um racional
por rnts » Seg Mai 21, 2012 16:15
- 1 Respostas
- 1713 Exibições
- Última mensagem por Guill

Sáb Mai 26, 2012 16:07
Álgebra Elementar
-
- Números irracionais
por cristina » Qua Set 16, 2009 23:40
- 1 Respostas
- 1976 Exibições
- Última mensagem por Marcampucio

Qui Set 17, 2009 00:18
Álgebra Elementar
-
- Números irracionais
por Marcia » Seg Nov 15, 2010 19:41
- 1 Respostas
- 1690 Exibições
- Última mensagem por Rogerio Murcila

Ter Nov 16, 2010 10:22
Álgebra Elementar
-
- números irracionais
por jose henrique » Sáb Fev 12, 2011 20:35
- 5 Respostas
- 5952 Exibições
- Última mensagem por Dan

Sáb Fev 12, 2011 21:39
Álgebra Elementar
-
- Números irracionais
por lacesar » Dom Abr 12, 2015 16:52
- 1 Respostas
- 2203 Exibições
- Última mensagem por adauto martins

Ter Mai 08, 2018 18:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[]{2}}{\sqrt[]{4}}= \frac{1}{\sqrt[]{2}} \frac{\sqrt[]{2}}{\sqrt[]{4}}= \frac{1}{\sqrt[]{2}}](/latexrender/pictures/d3e726b6485fda7dd3b31f9ebfd962cc.png)
![\frac{\sqrt[]{2}}{\sqrt[]{18}} = \frac{1}{\sqrt[]{9}} \frac{\sqrt[]{2}}{\sqrt[]{18}} = \frac{1}{\sqrt[]{9}}](/latexrender/pictures/244daba5ed16488e2e3dd603ace81888.png)
![\frac{\sqrt[]{16}}{\sqrt[]{36}} = \frac{2}{3} \frac{\sqrt[]{16}}{\sqrt[]{36}} = \frac{2}{3}](/latexrender/pictures/5bfa919ddf41a87177fd1580a73f06db.png)
![\frac{\sqrt[]{2}}{\sqrt[]{36}} = \frac{2}{6 \sqrt[]{2}} \frac{\sqrt[]{2}}{\sqrt[]{36}} = \frac{2}{6 \sqrt[]{2}}](/latexrender/pictures/a5ed910fefef5d9508f6763472c433f5.png)
![\frac{\sqrt[]{2}}{\sqrt[]{20}} = \frac{1}{\sqrt[]{10}} \frac{\sqrt[]{2}}{\sqrt[]{20}} = \frac{1}{\sqrt[]{10}}](/latexrender/pictures/37dc80f8b2d39ef5b8008b2553257adb.png)


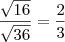
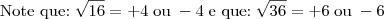

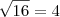 e
e 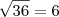 , obrigatoriamente.
, obrigatoriamente.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.