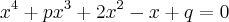 , apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1.
, apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1.gabarito:
 e
e 

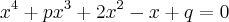 , apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1.
, apresente duas raízes recíprocas entre si e as outras duas com soma igual a 1. e
e 


 não deveria assumir o valor de
não deveria assumir o valor de  , e o
, e o  tbm? :/
tbm? :/
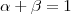
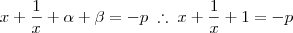
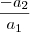 )
)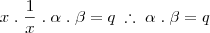
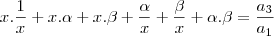
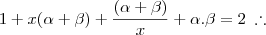

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante