tal que 
, para os quais a1, a2, a3 formam, nessa ordem, uma PG de razão e representam as medidas dos lados de um triângulo.gabarito:
![q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[](/latexrender/pictures/636ee168a27bde75c4f872fdd5246084.png "q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[")
por Carolziiinhaaah » Qua Jun 16, 2010 18:31
tal que , para os quais a1, a2, a3 formam, nessa ordem, uma PG de razão e representam as medidas dos lados de um triângulo.
por Douglasm » Qua Jun 16, 2010 20:56
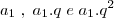(em ordem crescente, notando que os lados formam uma P.G.).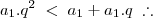
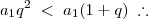
![\left]\frac{1-\sqrt{5}}{2} \; , \; \frac{1+\sqrt{5}}{2}\right[](/latexrender/pictures/a05a67dc7a982df24d0ff576dc47dd40.png "\left]\frac{1-\sqrt{5}}{2} \; , \; \frac{1+\sqrt{5}}{2}\right[")
. ![q \; \in \; \left]1 \; , \; \frac{1+\sqrt{5}}{2}\right[](/latexrender/pictures/a9d5b3d50488f849344068fca9076895.png "q \; \in \; \left]1 \; , \; \frac{1+\sqrt{5}}{2}\right[")
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)
Valeu Douglas!