 por Carolziiinhaaah » Qua Jun 16, 2010 14:07
por Carolziiinhaaah » Qua Jun 16, 2010 14:07
Mais uma de PG, gente..
Calcule o valor da soma de n parcelas 1 + 11 + 111 + ... + 111...1 ( n "uns" ).
gabarito:
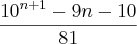
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Ter Jun 22, 2010 18:54
por Douglasm » Ter Jun 22, 2010 18:54
Nesse caso, é só reescrevermos da seguinte forma:
1 + 11 + 111 + 1111 + ... + 11111(n vezes) = 1 + (10 + 1) + (100 + 10 + 1) + ...
Deste modo vamos calcular a soma de cada uma dessas progressões (cada um dos fatores). Para o último fator:
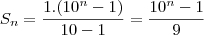
É evidente que para os outros fatores nós teremos:
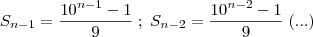
Somando isso tudo:
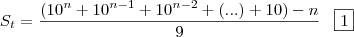
Agora temos uma outra progressão dentro dos parênteses:
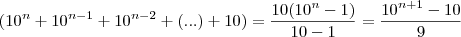
Finalmente, substituindo esse valor em "1":
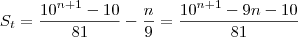
E está ai a resposta.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria] O menor valor possível para soma.
 por my2009 » Ter Fev 09, 2016 10:59
por my2009 » Ter Fev 09, 2016 10:59
- 1 Respostas
- 4580 Exibições
- Última mensagem por Baltuilhe

Sáb Fev 20, 2016 19:27
Geometria
-
- me ajudem calculos para antecipar parcelas
por MABafi » Dom Jul 18, 2010 23:36
- 0 Respostas
- 1610 Exibições
- Última mensagem por MABafi

Dom Jul 18, 2010 23:36
Matemática Financeira
-
- Matemática Financeira, a vista/parcelas diferentes
por med_amanda » Seg Set 30, 2013 18:44
- 0 Respostas
- 1192 Exibições
- Última mensagem por med_amanda

Seg Set 30, 2013 18:44
Matemática Financeira
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2101 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- Racionalização de denominador composto de "três parcelas"
por Jesse Pessoa » Sex Abr 01, 2011 21:59
- 8 Respostas
- 9749 Exibições
- Última mensagem por paulo testoni

Sex Nov 15, 2013 22:09
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
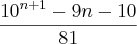

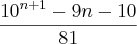

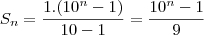
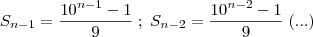
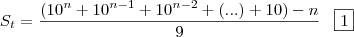
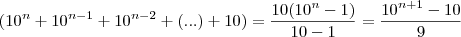
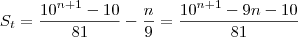



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.