Como chegou nesta unidade?

por **borges25borges** » Sáb Mai 31, 2008 16:43

Exercício 7.2. É desejável aquecer 9820 lb/h de benzeno ( cp = 0,425 Btu/lb.oF ) de 80 a 120 oF utilizando tolueno ( cp = 0,44 Btu/lb.oF ), o qual é resfriado de 160 para 100 oF. Um fator de fuligem de 0,001 deve ser considerado para cada fluxo e o coeficiente global de transferência de calor "limpo" é 149 Btu/h.ft2.oF. Dispõe-se de trocadores bitubulares de 20 ft de comprimento equipados com tubos área específica de 0,435 ft2/ft.
a) Qual a vazão de tolueno necessária?
b) Quantos trocadores são necessários?

a) A vazão de tolueno pode ser obtida realizando um balanço térmico :

b) Para obter o número de trocadores é necessário calcular a área de troca de calor necessária. O MLDT do trocador é obtido assim :

Cálculo do coeficiente global considerando o fator fuligem ( sujo ) :

1/Ud = 1/Uc + Rdi +Rde
Ud = 1/149 + 0,001 + 0,001
Ud = 115 Btu/h*ft²*°F

Cálculo da área de troca de calor :

O calor trocado é igual ao calor recebido pelo benzeno, portanto :

São necessários 50,5 m2 de área de troca de calor. Como os tubos do trocador dispõem de uma área por unidade de comprimento conhecida, é possível calcular o comprimento de tubo necessário :

Como cada trocador tem tubos de 20 ft de comprimento, o número de trocadores é :

Por favor como ele chegou nesta unidade, na parte que está resolvida do cálculo do coeficiente global considerando o fator fuligem

por **admin** » Sáb Mai 31, 2008 18:42

Olá borges25borges, boas-vindas!

Apenas considerando as operações matemáticas, a partir de onde você citou, sem adentrar nos detalhes físicos, pois não tenho competência para tal:

coeficiente global de transferência de calor "limpo": $149 \frac{Btu}{h\cdot ft^2 \cdot ^oF}$

$\frac{1}{U_d} = \frac{1}{U_c} + R_{di} + R_{de}$

$\frac{1}{U_d} = \frac{1}{149} + 0,001 + 0,001$

$U_d = 115 \frac{Btu}{h \cdot ft^2 \cdot ^oF}$

borges25borges, nestas situações onde queremos conferir a unidade obtida, meus professores do curso técnico em química sempre recomendavam "fazer as contas também com as unidades", como uma análise dimensional.

Então, vamos inserir a unidade de U_c

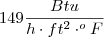
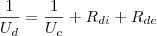
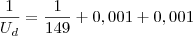
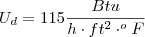
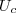na conta, considerando que o fator seja adimensional, veja: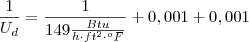

$\frac{1}{U_d} = \frac{1}{149 \frac{Btu}{h\cdot ft^2 \cdot ^oF}} + 0,001 + 0,001$

As operações com as unidades resultarão na unidade de U_d

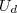, vamos aos passos: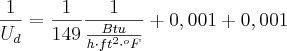

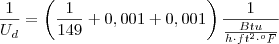
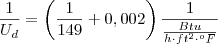
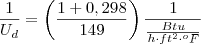
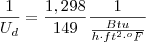
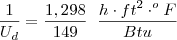
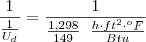
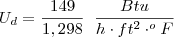
$\frac{1}{U_d} = \frac{1}{149} \frac{1}{\frac{Btu}{h\cdot ft^2 \cdot ^oF}} + 0,001 + 0,001$

A soma dos termos adimensionais não altera a unidade, então:

$\frac{1}{U_d} = \left( \frac{1}{149} + 0,001 + 0,001 \right) \frac{1}{\frac{Btu}{h\cdot ft^2 \cdot ^oF}}$

$\frac{1}{U_d} = \left( \frac{1}{149} + 0,002 \right) \frac{1}{\frac{Btu}{h\cdot ft^2 \cdot ^oF}}$

M.M.C.:
$\frac{1}{U_d} = \left( \frac{1+0,298}{149} \right) \frac{1}{\frac{Btu}{h\cdot ft^2 \cdot ^oF}}$

$\frac{1}{U_d} = \frac{1,298}{149} \frac{1}{\frac{Btu}{h\cdot ft^2 \cdot ^oF}}$

Fazendo o inverso da unidade:
$\frac{1}{U_d} = \frac{1,298}{149} \;\; \frac{h\cdot ft^2 \cdot ^oF}{Btu}$

Inverso dos dois membros da equação:
$\frac{1}{\frac{1}{U_d}} = \frac{1}{\frac{1,298}{149} \;\; \frac{h\cdot ft^2 \cdot ^oF}{Btu}}$

$U_d = \frac{149}{1,298} \;\; \frac{Btu}{h\cdot ft^2 \cdot ^oF}$

$U_d \approx 114,79 \;\; \frac{Btu}{h\cdot ft^2 \cdot ^oF}$

Espero ter ajudado!

por **borges25borges** » Sáb Mai 31, 2008 20:31

Muito obrigado Fábio, você acaba de me salvar na prova de Fenômenos dos Transportes 2. Valeuzão, desculpe pelo jeito que digitei as fórmulas, mas não consegui usar este programa latex.

Como chegou nesta unidade?

Como chegou nesta unidade?

Como chegou nesta unidade?

Re: Como chegou nesta unidade?

Re: Como chegou nesta unidade?

Quem está online