 por Nmdm » Seg Mai 24, 2010 12:29
por Nmdm » Seg Mai 24, 2010 12:29
Como resolver essa equação x2 + x +?(x2 + x + 10) =10 ?
Resp: {-3,2}
Já tentei resolver várias vezes, mas sempre chego numa eq. de 4 grau e não consigo resolver.
Me ajudem, por favor!!!
-
Nmdm
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Mai 24, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Douglasm » Seg Mai 24, 2010 13:52
por Douglasm » Seg Mai 24, 2010 13:52
Olá Nmdm. Para resolver essa equação, é conveniente usar uma substituição. Façamos:
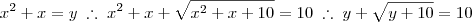
Agora podemos elevar os dois membros ao quadrado e resolver para y:
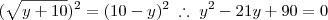
Essa nova equação tem raízes:


Mas notemos que a primeira equação,

, é uma equação do primeiro grau e, portanto, apresenta apenas uma raiz. Ao substituirmos ambos os valores, encontramos que a única raiz é 6. Veja só:
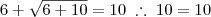
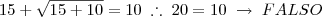
Agora é só fazermos a substituição:
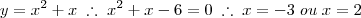
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações irracionais
por LuizCarlos » Qui Mai 17, 2012 00:12
- 2 Respostas
- 1326 Exibições
- Última mensagem por LuizCarlos

Qui Mai 17, 2012 12:50
Álgebra Elementar
-
- [Números Irracionais] Soma de irracionais dando um racional
por rnts » Seg Mai 21, 2012 16:15
- 1 Respostas
- 1713 Exibições
- Última mensagem por Guill

Sáb Mai 26, 2012 16:07
Álgebra Elementar
-
- Números irracionais
por cristina » Qua Set 16, 2009 23:40
- 1 Respostas
- 1977 Exibições
- Última mensagem por Marcampucio

Qui Set 17, 2009 00:18
Álgebra Elementar
-
- Números irracionais
por Marcia » Seg Nov 15, 2010 19:41
- 1 Respostas
- 1692 Exibições
- Última mensagem por Rogerio Murcila

Ter Nov 16, 2010 10:22
Álgebra Elementar
-
- números irracionais
por jose henrique » Sáb Fev 12, 2011 20:35
- 5 Respostas
- 5955 Exibições
- Última mensagem por Dan

Sáb Fev 12, 2011 21:39
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



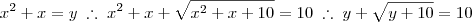
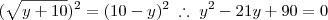


 , é uma equação do primeiro grau e, portanto, apresenta apenas uma raiz. Ao substituirmos ambos os valores, encontramos que a única raiz é 6. Veja só:
, é uma equação do primeiro grau e, portanto, apresenta apenas uma raiz. Ao substituirmos ambos os valores, encontramos que a única raiz é 6. Veja só: 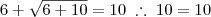
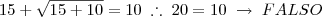
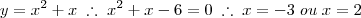

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.