 por Cleyson007 » Sáb Mai 24, 2008 23:30
por Cleyson007 » Sáb Mai 24, 2008 23:30
Olá Fábio Sousa, boa noite!!!
Gostaria de compartilhar o modo que resolvi o exercício abaixo e saber se o procedimento por mim adotado se está correto.
Desde já agradeço por sua ajuda e pela ajuda de todos os que fazem desse site um grande e rico espaço de aprendizado.
Questão: Insira sete meios aritméticos entre 20 e 68.
Eu resolvi assim: ---> Coloquei como o termo geral o 68. Como o 1º termo o 20. Como o nº de termos o 07, e procurei a razão (r).
Ficou assim: 68 = 20+ (7-1)r 68 - 20= 6r 48 = 6r r=8
S: { 21,28,35,42,49,56,63}
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Sáb Mai 24, 2008 23:35
por Cleyson007 » Sáb Mai 24, 2008 23:35
Cleyson007 escreveu:Olá Fábio Sousa, boa noite!!!
Gostaria de compartilhar o modo que resolvi o exercício abaixo e saber se o procedimento por mim adotado se está correto.
Desde já agradeço por sua ajuda e pela ajuda de todos os que fazem desse site um grande e rico espaço de aprendizado.
Questão: Insira sete meios aritméticos entre 20 e 68.
Eu resolvi assim: ---> Coloquei como o termo geral o 68. Como o 1º termo o 20. Como o nº de termos o 07, e procurei a razão (r).
Ficou assim: 68 = 20+ (7-1)r 68 - 20= 6r 48 = 6r r=8
S: { 21,28,35,42,49,56,63}
Coloquei a solução de outro exercício que estava resolvendo aqui, a solução que encontrei para esse foi:
S: {20,28,36,44,52,60,68}
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Dom Mai 25, 2008 01:22
por admin » Dom Mai 25, 2008 01:22
Olá Cleyson, boa noite!
A idéia é esta, mas a resolução não está correta porque você confundiu o número de termos.
Se vamos inserir 7 termos entre outros 2, o total de termos será 9.
Cleyson007 escreveu:Coloquei como o termo geral o 68
Não é correto falar assim, porque o termo geral é
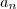
.
68 é o 9º termo, ou seja,

.
Então, apenas refaça as contas para encontrar a razão, considerando 9 termos, sendo

e

.
Espero ter ajudado.
Até mais! Bom domingo!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Dom Mai 25, 2008 02:09
por Cleyson007 » Dom Mai 25, 2008 02:09
fabiosousa escreveu:Olá Cleyson, boa noite!
A idéia é esta, mas a resolução não está correta porque você confundiu o número de termos.
Se vamos inserir 7 termos entre outros 2, o total de termos será 9.
Cleyson007 escreveu:Coloquei como o termo geral o 68
Não é correto falar assim, porque o termo geral é
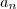
.
68 é o 9º termo, ou seja,

.
Então, apenas refaça as contas para encontrar a razão, considerando 9 termos, sendo

e

.
Espero ter ajudado.
Até mais! Bom domingo!
Considerando que já existem dois termos inclusos na PA (20 e 68), a resolução ficaria assim?
68 = 20 + (9 - 1) r
r = 8s: {20,28,36,44,52,60,68}
Boa noite!!!
Forte abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Dom Mai 25, 2008 02:19
por admin » Dom Mai 25, 2008 02:19
Cleyson007 escreveu:Considerando que já existem dois termos inclusos na PA (20 e 68), a resolução ficaria assim?
68 = 20 + (9 - 1) r r = 8
s: {20,28,36,44,52,60,68}
Cleyson, a sua equação para o 9º termo está certa, mas não calculou a razão corretamente.
E repare que neste seu último conjunto ainda há 7 termos.
Serão 9 termos no total: os 2 extremos + os 7 inseridos.
Confira sua conta a partir daqui:

Depois, obtenha os 9 termos corretos.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Dom Mai 25, 2008 12:33
por Cleyson007 » Dom Mai 25, 2008 12:33
fabiosousa escreveu:Cleyson007 escreveu:Considerando que já existem dois termos inclusos na PA (20 e 68), a resolução ficaria assim?
68 = 20 + (9 - 1) r r = 8
s: {20,28,36,44,52,60,68}
Cleyson, a sua equação para o 9º termo está certa, mas não calculou a razão corretamente.
E repare que neste seu último conjunto ainda há 7 termos.
Serão 9 termos no total: os 2 extremos + os 7 inseridos.
Confira sua conta a partir daqui:

Depois, obtenha os 9 termos corretos.
68 - 20 = 8r 48 = 8r
r = 6S: { 20,26,32,38,44,50,56,62,68}
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Dom Mai 25, 2008 12:38
por admin » Dom Mai 25, 2008 12:38
Olá Cleyson, bom dia!
Isso mesmo, estes são os 9 termos da progressão aritmética de razão 6.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Problemas aritméticos] As 4 operações
por delta110688 » Seg Fev 04, 2013 23:39
- 2 Respostas
- 1490 Exibições
- Última mensagem por delta110688

Qua Fev 06, 2013 03:12
Aritmética
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11058 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida sobre PA
por Cleyson007 » Ter Mai 27, 2008 23:22
- 3 Respostas
- 5005 Exibições
- Última mensagem por admin

Sáb Mai 31, 2008 21:57
Progressões
-
- duvida sobre mmc e mdc
por edson cesar » Ter Dez 07, 2010 09:10
- 0 Respostas
- 2082 Exibições
- Última mensagem por edson cesar

Ter Dez 07, 2010 09:10
Sistemas de Equações
-
- Duvida sobre EDO
por manolo223 » Dom Nov 13, 2011 00:19
- 2 Respostas
- 2425 Exibições
- Última mensagem por manolo223

Dom Nov 13, 2011 13:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
. .
. e
e 

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
